Inscription / Connexion Nouveau Sujet
Exercice sur Torseur cinématique et angle d'Euler
Bonjour,
Je pense avoir du mal à appliquer certains théorème liés au Torseur cinématique, je vous mets l'énoncé de l'exercice d'abord :
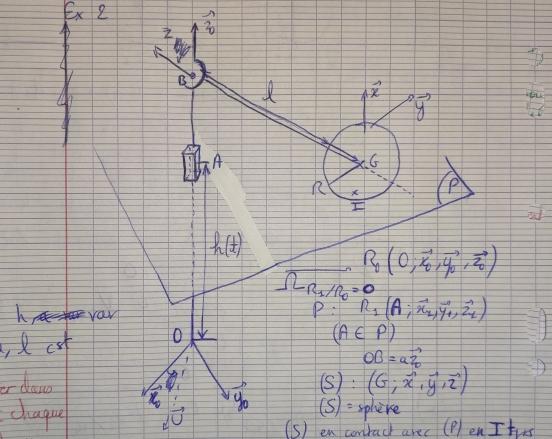
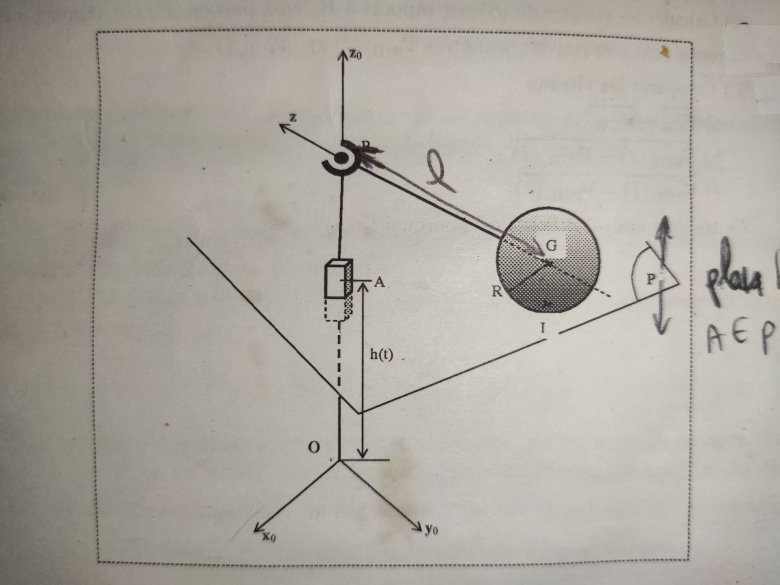
"Soit R0(O; x0,y0,z0) un trièdre orthonormé direct. Un plan (P) rapporté au trièdre orthonormé direct R1(A;x1,y1,z1) est animé d'un mouvement de translation rectiligne par rapport à R0 de façon que : OA = h(t)z0 et x1=x0, z1=z0
On considère d'autre part le solide (S) constitué par une sphère de centre G, de rayon R, sur laquelle est soudée une tige matérielle d'extrémité b; Le solide S est rapporté au trièdre orthonormé direct (G;x,y,z) tel que : z= GB/l où l = module(GB) (l>R).
On impose au solide S la liaison suivante : OB = az0, avec a constante.
L'orientation du solide S par rapport à R0 est repérée par les angles d'Euler habituels ψ,θ, φ.
On suppose de plus, qu'à tout instant t, le solide S est en contact avec le plan P en un point Ɪ , point de contact entre la surface de la sphère et le plan.
Q1 : Calculer les vitesses de G par rapport à R0 et R1
Q2 : Calculer les vitesses de Ɪ par rapport à R0, R1 et S
Pour VꞮ/R1, je trouve VꞮ/R1= -l[ψ(.)z0+θ(.)u]∧z - h(.)z0 = VG/R1, mais quand j'essaye de retrouver le même résultat via Varignon j'ai VꞮ/R1 = VG/R1 + OMEGAS/R1 ∧ GI avec le second terme nul du coup, mais est-ce qu'on peut dire que ce second terme est nul parce que OMEGAS/R1 ∧ GI = [d(R1)/dt]*(GꞮ ) ? D'un côté j'ai l'impression qu'on peut appliquer ce théorème parce que GꞮ semble lié à S ( car G est lié à S et Ɪ aussi car pt de contact ) mais d'un autre côté on a GꞮ = -Rz0 et z0 est lié à R0 et R1, mais pas à S.
Pour VꞮ /S, comme Ɪ est lié à S j'ai envie de dire 0 mais ça me paraît incohérent puisqu'on a un roulement sans glissement donc VS/R1(Ɪ) = 0 (car P lié à R1) et donc VꞮ/S=VꞮ/R1.
Merci de votre aide.
Scanner les énoncés de moins d'une page est interdit. Scanner les schémas est recommandé. L'énoncé est sans doute accompagné d'un schéma. Tu pourrais le scanner en complément du tien ?
La liaison en B est bien une liaison rotule ? Il faudrait aussi que tu indiques sur ta figure clairement, les angles et leurs orientations. Impossible sinon de vérifier tes résultats. Je peux tout de même, je crois, répondre à ton interrogation.
L'énoncé parle de contact en I mais ne précise pas que la boule (S) roule sans glisser sur le plan (P). Il faut donc considérer deux vitesses de I/R1 :
1° / La vitesse de I considéré comme appartenant à la boule (S) :
2° / La vitesse de I considéré comme appartenant au plan P qui, évidemment, est nulle dans R1. La différence entre les deux étant la vitesse de glissement de (S) par rapport à (P)
On peut évidemment imaginer un point H, qui se déplace dans le plan (P) en restant constamment à la verticale du point G. Ce point a même vitesse que G mais ce point n'appartient ni à la boule (S) ni au plan (P) au sens habituellement donné au verbe "appartenir" en mécanique du solide.
Merci, B est une liaison rotule oui, et en fait les angles sont les angles d'Euler (avec psi l'angle de précession autour de z0, theta l'angle de nutation et phi l'angle de rotation propre (comme sur wikipedia mais avec leur Z qui est z0 ici et leur Z' qui est z ici). donc on ne les connaît pas et du coup je ne sais pas comment mettre les angles sur mon schéma, j'ai juste theta =(z0,z).
J'ai une autre question, pourquoi à la question 1 on peut appliquer ce théorème alors que GI n'est pas lié à S, mais à R0 et R1 ( car GI = -Rz0 ) ? Du coup pour la liaison du vecteur à un repère, c'est les points qui le définissent qui compte (G et I), et pas le vecteur appartenant à un repère selon lequel ils sont exprimés (z0) ?
Ill y a des subtilités dans tout cela et c'est vraiment bien que tu te poses toutes ces questions !
La relation de Varignon est applicable ici dans R1 car G et I sont deux points appartenant au solide (S). Le point I n'est donc pas toujours dans le plan (P) au cours du temps. On se contente simplement d'exprimer la vitesse d'un point à la périphérie de la boule dans le cas particulier où ce point correspond au contact entre la boule et le plan. Le vecteur n'est donc pas un vecteur fixe au cours du temps dans R1.
Pour te convaincre de cela, tu peux remarquer :
C'est un peu comme si on te demandais d'étudier le mouvement d'un point à la périphérie d'une roue. Le point considéré décrit une cycloïde, sa vitesse varie au cours du temps de façon assez complexe. Très souvent on se limite à exprimer la vitesse de ce point dans le cas particulier où il est en contact avec le plan de roulement : cette vitesse est nulle en absence de glissement.
Désolé de remonter le sujet mais je n'ai toujours pas compris, même après avoir refais plusieurs fois l'exercice, justement je trouve VꞮ/R1= -l[ψ(.)z0+θ(.)u]∧z - h(.)z0 = VG/R1 et c'est la même chose que le prof a trouvé du coup je suis perdu...
J'ai aussi l'impression que GꞮ est fixe par rapport à R1 et R0 puisque GꞮ = -Rz0, et z0 est lié à R0 et R1...
Pourriez vous m'expliquer avec des exemples peut-être plus simple, comment déterminer à quel solide/repère est lié un vecteur AB quelconque (si c'est en priorité par rapport aux points AB, comme vous le dites mais contraire à la correction de mon prof, ou par rapport au vecteur de repère avec lequel il est exprimé) ?
Merci encore.
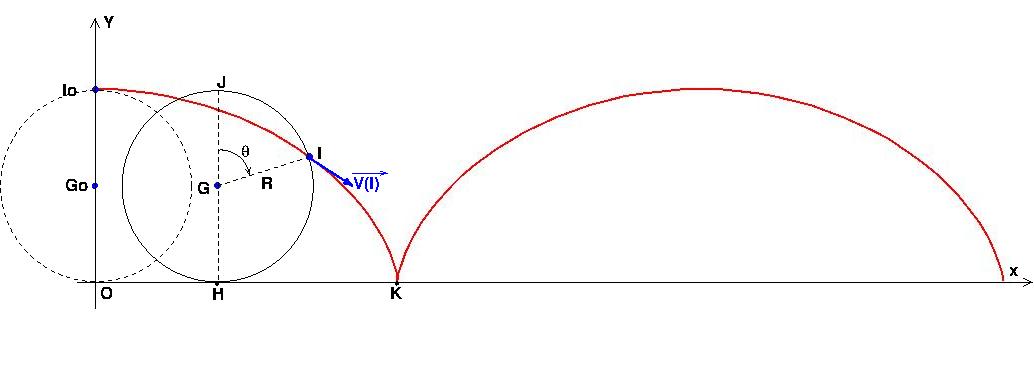
Tu n'as effectivement pas compris mon message précédent... Je retente ma chance en m'aidant d'un schéma. Il correspond à une roue assimilée à un disque de centre G et de rayon R roulant sans glisser sur un plan horizontal. C'est une situation plus simple mais on y rencontre la même difficulté de compréhension...
On peut effectivement définir un point du plan de roulement (de l'axe Ox de mon schéma) situé à chaque instant à la verticale du point G. Evidemment ce point se déplace par rapport au plan de roulement à la même vitesse que G. Je l'ai appelé H, tu peux l'appeler Ɪ si tu veux. Attention : ce point n'est fixe ni par rapport au plan de roulement, ni par rapport à la roue. Il est donc normal que la relation de Varignon ne s'applique pas à ce point.
Soit maintenant un point I à la périphérie de la roue et fixe par rapport à la roue. Ce point décrit une cycloïde (tracée en rouge) et sa vitesse vérifie la relation de Varignon à chaque instant.
On peut bien sûr exprimer à l'aide de la relation de Varignon la vitesse de I lorsque I entre en contact avec le plan de roulement (I en K, G à la verticale de K). Bien sûr, dans ce cas : mais cela ne veut pas dire que le vecteur
est un vecteur fixe : avant et après l'instant de passage de I en K, le vecteur
n'est pas vertical, son inclinaison dépend de l'angle
 qui varie au cours du temps.
qui varie au cours du temps.
D'ailleurs, la vitesse de I dans le cas particulier où I passe par K est le vecteur nul alors que la vitesse de G n'est pas nulle.