Inscription / Connexion Nouveau Sujet
Exercice sur les transferts thermiques
Bonjour à tous, on m'a posé l'exercice suivant :
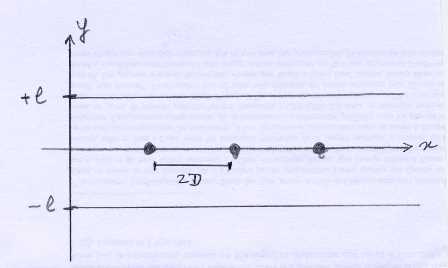
On considère une plaque de céramique délimitée par les plans et
en contact avec des fils qui vont lui communiquer de la chaleur espacés d'une longueur
selon l'axe
.
On connait la température extérieure, notée . La plaque de céramique a une conductivité
Chaque fil est de section , de conductivité thermique
.
1) Quelle est l'intensité parcourant le fil connaissant la puissance thermique par unité de longueur de fil ?
2) Déterminer la température à l'intérieur de la céramique. On supposera infinie.
3) On ne suppose plus que est infinie. En réalisant des simplifications adaptées, déterminer la température à l'intérieur de la céramique.
1) Pour une longueur de fil :
Où :
D'où
2)
D'après la loi de Fourier,
Comme ne peut pas être infini,
= 0
ce qui nous donne
D'après l'équation de la chaleur, sachant que les fils sont des sources intérieures
est de la forme :
, où
On utilise les conditions aux limites :
Et là je ne comprends pas où je me suis trompée...
bonjour,
dans le 2) si la température est uniforme on obtient une équation du genre:
 Cp V dT/dt = P - Pdissipée
Cp V dT/dt = P - Pdissipée
il manque la puissance dissipée par la plaque, par ex. par convection à la surface elle serait de la forme: hS(T-Te)
sinon la température va tendre vers l'infini !
sauf erreur
Merci de ta réponse.
En fait, je ne sais pas du tout comment exprimer la production volumique de chaleur.


