Inscription / Connexion Nouveau Sujet
exercice sur les forces
Bonjour, J'aurais besoin de conseils pour un exo de physique, surtout sur les méthodes à utiliser:
Un solide de masse m peut glisser sans frottement sur un plan incliné
d'un angle a par rapport à l'horizontale. Il est maintenu en équilibre par
un ressort qui exerce sur lui une tension notée T. Le support exerce sur la
masse m une force notée R perpendiculaire au plan incliné.
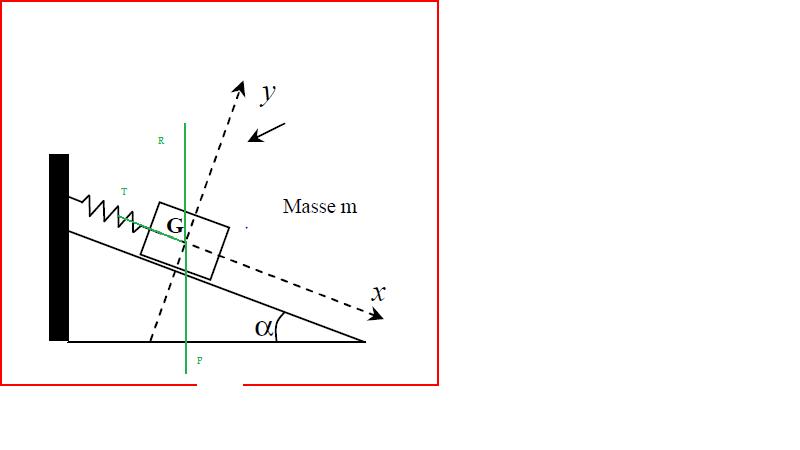
a) Représenter en vert sur le schéma ci-contre et sans tenir compte de leur
intensité les forces extérieures appliquées au solide à partir de G.
b) Exprimer les composantes du vecteur poids P dans le repère ( G; x, y )
en fonction de m, g et a.
c) En déduire de même celles de la tension T du fil et de la résistance R du
support en détaillant la démonstration.
d) On donne m = 250 g et a = 25°. Calculer les intensités R et T.
e) En prenant comme tension du ressort T = 2,0 N déterminer la raideur k du
ressort sachant que son allongement dû à la masse m est de 1,1 cm.
merçi d'avance
Bonsoir, j'ai fait des corrections détaillées de ce genre d'exos.
Utilise l'outil rechercher pour les retrouver 
merçi j'ai regardé mais y'avit pas de composantes de vecteurs 
Peux tu m'expliquer comment il faut faire ?
quelqu'un peut me dire si le schéma est juste ?( je n'ai pas pu faire les flèches et celles des vecteurs)
Merçi d'avance
ah oui !!! je ne le remets pas sur le dessin, j'ai des problèmes pour ouvrir paint. ( R serait donc au niveau de l'axe des ordonnées)
pour la b/ je propose Px= mg.cosa
Py=-mg
c/ Tx=-mg.sin(a)
Ty=0
Rx= 0
Ry= mg
d/ je bloque (enfin peut être que c'est faux au dessus)
e/ j'ai trouvé 181.81 N
quelqu'un peut confirmer et m'expliquer svp
b. pour Px, ok
pour Py = - m g sin a
c. pour T, ok
pour R, non (voir question b. )
d. Comment peux-tu bloquer, il faut faire le calcul, non ?
e. Es-tu sûr de l'unité ? Peux-tu mettre le détail du calcul ?
pour la d/ il s'agit d'une formule ou il faut faire la norme des vecteurs avec  x²+y²
x²+y²
(je n'ai pas encore fait le cour en entier)
c/R (donc axe des ordonnées)
Rx=0
Ry= mg
e/j'ai fait K= T/(L-L0)
K=2/0.011=181.81 N/M
merçi
b)composantes du vecteur poids dans le repère ( G; x, y )
Px=+P.sina
Py=-Pcosa
c) composantes de dans le repère ( G; x, y )
Rx=0
Ry=+R
composantes de dans le repère ( G; x, y )
Tx=-T
T=0
d) équilibre => 
=> Px+Rx+Tx=0 et Py+Ry+Ty=0
Px+Rx+Tx=0 => +P.sin(a)+0-T=0 => T=mgsin(a)=0,25kg.9,81N/kg.sin25 1N
1N
c)et d)
Py+Ry+Ty=0 =>-Pcos(a)+R+0+0 +> R=mgcos(a)=0,25kg.9,81N/kg.cos25 2,2N
2,2N
e) K=2/0,011=181,8 N/m