Bonjour Joaninha,

une frange brillante est une zone de l'écran d'observation où il y a un maximum d'intensité lumineuse ; une frange sombre, au contraire, est une zone où il y a un minimum de lumière. Si ces zones sont des droites, on parle de franges. Avec d'autres systèmes interférentiels elles peuvent être des cercles concentriques : on parle alors d'anneaux sombres ou brillants. Curieux que tu ne sache pas ce qu'est une frange, car c'est au programme de Terminale S, mais peu importe.
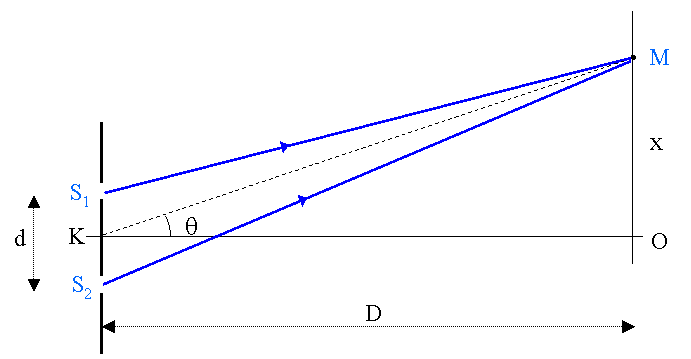
Sur le schéma ci-dessous j'ai résumé la situation : en effet un calcul simple et sans intérêt montre que S₂M - S₁M = r₂ - r₁ vaut d, à condition que l'angle soit suffisamment petit pour qu'on puisse confondre sa valeur en radians avec son sinus ou sa tangente. Cette différence des distances S₂M - S₁M s'appelle différence de marche, notée . Avec x/D = tan , on obtient = ax/D. OK jusqu'ici ?

Appelons E(t) l'onde émise par une source monochromatique S : E(t) = E₀.cost, avec = 2/T ( : pulsation de l'onde, T : sa période). Cette onde se propage dans l'espace à la vitesse c si on est dans le vide (on va garder cette hypothèse pour cet exercice, le cas d'une onde se propageant dans un milieu matériel pourra éventuellement être vu plus tard).
Voici un raisonnement très simple qui devrait t'aider à t'y retrouver dans ce genre de problèmes, avec un minimum de calculs mathématiques :

Supposons que l'onde E(t) arrive en un point M situé à la distance r = SM de la source. Pour écrire l'état vibratoire de l'onde en M, il suffit de dire que ce qui se passe en M à l'instant s'est passé en S à l'instant t - t0, t0 étant le temps mis par cette onde pour parcourir la distance SM. Donc E_M(t) = E₀.cos(t-t₀).
Avec t₀ = r/c, on obtient facilement t₀ = 2r/cT = 2r/, où = cT est la longueur d'onde de cette onde.
On arrive donc à E_M(t) = E₀.cos(t - ), avec = 2r/. représente le déphasage de l'onde arrivant en M par rapport à celle qui a quitté la source S. Le signe - indique que ce déphasage correspond bien évidemment à un retard. OK ? pas de panique, on avance.

Maintenant, prenons le cas de deux ondes arrivant en M, l'une provenant d'une source S₁ située à la distance S₁M = r₁, l'autre d'une source S₂ distante de S₂M = r₂. Plaçons-nous dans le cas où les deux ondes, de même amplitude E₀, ont quitté leurs sources respectives en même temps : on dit aussi que les sources S₁ et S₂ sont synchrones (dans des exercices où ce n'est pas le cas... plus tard stp). Les deux ondes qui arrivent en M s'additionnent et on peut écrire :
E_M(t) = E_1M(t) + E_2M(t) = E₀[cos(t - ₁) + cos(t - ₂)].
En math on voit une relation de trigonométrie pour additionner deux cosinus : elle s'écrit cosp + cosq = 2.cos((p+q)/2].cos((p-q)/2] (formulaire très pratique éventuellement disponible ici : ). En posant t - ₁ = p et t - ₂ = q, tu vérifieras qu'on obtient sans difficulté
cos(t - ₁) + cos(t - ₂) = 2.cos[(₂-₁)/2].cos[t - (₁+₂)/2].

Le deuxième cosinus, celui qui contient le terme en t, varie très rapidement avec le temps (à cause de la pulsation ) : il traduit le fait que la vibration en M est bien sinusoïdale. On peut l'oublier car il va disparaître lorsqu'on prendra la valeur moyenne temporelle (<E²> dans ton cours). En revanche le premier est très important car il ne dépendant pas du temps, donc il intervient dans l'amplitude de l'onde résultante.
Reprenons les relations vues ci-dessus : avec ₂-₁ = 2(r₂-r₁)/ = 2/, on obtient le résultat très important suivant pour cette amplitude :
          E_M = 2.E₀.cos(/).

L'intensité lumineuse I en M est mesurée par le carré de cette amplitude (<E²>), on arrive finalement à

          I(M) = 4.I₀.cos²(/), avec I₀ = E₀ ² l'intensité lumineuse de chacune des sources.

Ouf, le plus dur est fait... Il ne reste plus qu'à étudier les maxima de cette expression pour obtenir les franges brillantes, et les minimas pour obtenir celle des franges sombre. Or la fonction cos² est maximale pour = 0, , ... k., où k est un entier relatif ou nul, et elle s'annule pour = /2, ... 3/2, ... (2k+1)/2, k étant aussi un entier relatif. D'où la position des franges :

*/  franges brillantes : / = k soit = k ;

*/  franges sombres : / = (2k+1)/2 soit = (2k+1)/2

On retrouve bien les propriétés vues sans démonstration en terminale S : si la différence de marche est un multiple de la longueur d'onde, les ondes arrivant en M ajoutent leurs amplitudes et on a un maximum de lumière en M ; si est un nombre impair de fois la demi-longueur d'onde, leurs amplitudes se retranchent et on a une frange sombre;

Pour savoir ce qui se passe sur l'écran d'observation, il ne te reste plus qu'à écrire que = dx/D et tu auras la position des points M correspondants. Tu peux également calculer la distance entre deux franges (brillantes ou sombres), appelée interfrange.

Bon, je crois qu'on a fait le tour de la question. A moi maintenant de t'en poser une : que vient faire cet exercice d'optique dans un cours sur la relativité ? La théorie de la relativité restreinte a bien pour point de départ une expérience d'interférence (qui s'est en fait passée pas comme prévu), mais par avec des fentes de Young.

Si tu as des questions (mon texte ci-dessus est certes un peu long, mais à la portée d'une élève de licence), n'hésite pas à les poster.