Bonjour/Bonsoir,  j'ai un exercice pour les vacances et j'aimerais bien avoir de l'aide pour quelques questions ; désolé pour la longueur de l'exo ^^' .

Exercice:
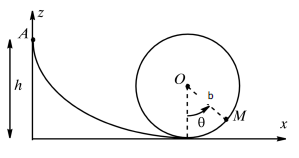
Un skate-boarder "de l'extrême" souhaite réaliser une performance exceptionnelle : il envisage de s'élancer sans vitesse initiale depuis le haut d'une rampe à l'altitude h (point A), de se laisser glisser, puis de terminer sa course par une grande boucle (un looping) de rayon fixe b. Plus l'altitude h est petite, plus la performance sera remarquable ! Cependant le skate-boarder n'est pas téméraire : il souhaite calculer au préalable l'altitude h minimale pour être certain de ne pas "décrocher" dans le looping.
Le référentiel d'étude, dans lequel la rampe et le looping sont fixes, est supposé galiléen.
On note g l'intensité du champ de pesanteur.
1) Dans un premier temps, on s'intéresse au mouvement du skate-boarder, assimilé un point matériel de masse m, évoluant à l'intérieur d'une sphère de rayon b, le mouvement se faisant sans frottement.
a) Faire le bilan des forces appliquées au skate-boarder lorsqu'il est au point M du schéma.
b) Ecrire l'équation fondamentale de la dynamique.
Soient vM la vitesse au point M et q l'angle entre la verticale et OM (voir le schéma).
Que devient cette équation en la projetant sur les vecteurs de base de Frenet ?
Exprimer la réaction normale en fonction de v_M, m, g et q.
Quelle est la condition sur cette réaction pour que le skate-boarder ne « décroche » pas ?
En déduire une condition sur v_M.

2) Dans un second temps, on étudie le mouvement depuis le haut de la rampe de lancement, le mouvement se faisant toujours sans frottement.
a) Faire le bilan des forces appliquées au skate-boarder sur la rampe de lancement.
Donner les expressions des énergies potentielles pour chaque force conservative.
b) Les forces agissant entre A et M sont-elles toutes conservatives ? Justifier.
Exprimer en fonction de b, h, g et q la norme vM de la vitesse du point M.
c) En quel point du looping la vitesse est-elle la plus faible ?
Exprimer cette vitesse minimale en fonction de g, h et b.

Mes réponses:

1)a) Système : {le skate-boarder}
Le référentiel d'étude est supposé galiléen.
Bilan des forces : le poids P et la réaction normale à la grande boucle R_n.
b) D'après de le principe fondamentale de la dynamique:
+ _n=m*
Après projection sur le repère de Frenet :
Sur u_T:
(sin)*P=m*(dv_M/dt)
Sur u_N:
(cos)*P+R_n=m*(v_M²/R)

Donc on en déduit que R_n=m(v_M/R - (cos)*g)

2)a) Système: {le skate-boarder}
Le référentiel terrestre est considéré galiléen.
Bilan des forces:
-le poids
-la réaction normale à la rampe _h

J'espère que mes réponses sont justes sinon j'aimerais une piste pour les corriger.

Je n'y arrive pas pour les questions:

1)b) Pour "Quelle est la condition sur cette réaction pour que le skate-boarder ne « décroche » pas ?
En déduire une condition sur v_M."

2)a) Donner les expressions des énergies potentielles pour chaque force conservative.
2)b) et 2)c)