Inscription / Connexion Nouveau Sujet
exercice - moteur a courant continu
Bonjour,
L'objectif est de déterminer les grandeurs suivantes de la MCC (voir schéma ci joint):
1) Le courant d'induit I1 nécessaire à faire monter la charge:
on sait que l'equation de la tension U (regime permanent est la suivante:
U=RI + Ku phi *omega
omega (vitesse angulaire 2*pi*n)
cependant je trouve une intensité trop élevé (environ 7000, ce qui est impossible)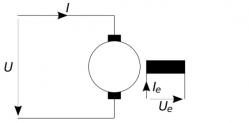
2)La constante de tension induite du moteur "ku" :
l'equation est la suivante:
Ku phi = U / omega
Cependant il faut utiliser la tension de l'induit et non U=500V.
Comment calculer la tension de l'induit?
3) La vitesse de rotation du moteur n2 à la descente:
nous avons v2 = 8m/s, la méthode pour trouver la vitesse de rotation n2 devrait être la suivante:
v2= R * w
R-> diametre arbre moteur
w-> 2*pi* n2
je ne peut pas utiliser cette methode car nous ne connaissons pas le diametre de l'arbre
du moteur
Si quelqu'un à une idée pour les 3 questions, car je suis vraiment bloqué
merci d'avance
Bonsoir
A ce que je comprends, U=500V est bien la tension aux bornes de l'induit. Ce moteur fournit une puissance mécanique considérable : Pm=105W. Il est donc normal que l'induit soit parcourue par un courant de forte intensité mais, personnellement, j'obtiens une valeur très inférieure à 700A.
Peux-tu expliquer ta démarche ?
Tu as bien converti les tours/min en rad/s ?
Je confirme le calcul suivant pour I1:
n1 = 750 tr/min
avec omega = (2*pi*n1)/60 = 78,53 rad/s
I1 = (U - Ku phi * omega) / R = 5268 A
Pour moi ce calcul est faux car la valeur du courant dans l'induit est trop importante
Ton hydroxyde est fausse.
Il faut raisonner sur la puissance.
La puissance électrique reçue pzrl" linduit est égale à U.I.
C'est la somme de deux puissances
La puissance mécanique connue
La puissance perdue par effet Joule R.I2
Celà te donne une équation du second degré dont I est solution.
Ok si je comprends bien en faisant le bilan des puissance d'une MCC à exitation séparée nous avons:
P électrique = U x I
P mécanique = T (couple) x omega
U= 500 V
P meca = 100000 W
omega = (2* pi * 750)/ 60 = 78,53 rad/s
T = Pmeca / omega = 1273, 39 N/M
En cherchant, j'ai constaté que la puissance elec (en entrée) est égale à la somme des pertes (joules et fer) et la Pmec (qui est connu)
Pelec = Pj + Pmec
Pelec = Rinduit x (I1^2) + Pmeca
Pelec = 0,08 x (I1^2) + 100000
C'est bien ça?
Que veut tu dire par "La puissance électrique reçue pzrl"?
Bug de ma part avec mon portable. Tu sais quand-même que puissance électrique reçue par l'induit est égale au produit U.I
Oui mais ici on peut pas calculer I1 = P/Uinduit, l'intensité serait de 200A (beaucoup trop élevé) car la Pmeca est la puissance en sortie
Dans ton équation traduisant le bilan de puissance posté à 16h06, il suffit de remplacer Pelec par U.I=500.I pour obtenir l'équation du second degré dont I est solution.
Cela conduit à une valeur de I un peu supérieure à 200A... une puissance de sortie de 105W, cela ne correspond pas à un moteur de machine à laver !
Je crois que j'ai trouvé:
on a:
Pelec = Rinduit * I1^2 + Pmec
500I1 = 0,08*I1^2 + 100000
on a une equation de second membre sous forme:
bx = ax^2 + c
0 = ax^2 +c -bx
a = 0,08
b = 500
c = 100000
delta = b^2 -4ac
delta = 218000
I1 = -b + racine(delta) / 2a
I1= (-(-500) + 466,904) / 0,16
I1 = 206,25 A
Ensuite on calcul la constante de tension induite ku:
ku = Cn /I1
omega = (2* pi * 750)/ 60 = 78,53 rad/s
Cn = Pmeca / omega (n1)= 1273, 39 N/M
ku = Cn / I1
ku = 1273,39 / 206,25
ku= 6,17 vs/rad
concernant la question 3 (determiner a vitesse de rotation du moteur n2 à la descente avec v2 = 8m/s), la formule est la suivante:
n2 = n1 * (1- (R*I1)/U))
n2= 750 * (1 - (0,08x206,25)/500))
n2= 750 * (1 - 0,033)
n2 = 725,25 tr/min
sachant que n1 correspond à une vitesse de 10/ms. Le résultat me paraît coherent
Pouvez vous confirmer, la question 2 et 3?
Merci encore pour votre support
Message de 22h06
Raisonnement correct mais attention aux unités. Un moment de couple se mesure en newtonmėtre (N.m).
Unité de ku ?
Pas d'accord avec ton dernier message. La vitesse angulaire est, pour un même dispositif, proportionnelle à la vitesse linéaire. La nouvelle valeur de oméga est donc la valeur précédente multipliée par 0,8.
Pour une même charge, la puissance mécanique est proportionnelle à la vitesse. Elle vaut donc la valeur précédente multipliée par 0,8.
Il suffit donc de reprendre le calcul précédent avec ces deux nouvelles valeurs, la tension U étant inchangée.
Pour la question 3, le calcul est le suivant:
n2 = n1 * (v2/v1)
n2 = 750 * (8/10)
n2= 600 tr/min
Merci encore pour votre support
A bientot
Pour cette exercice, il reste une grandeur à calculer: La resistance additionnelle Rd:
Le courant induit (I1 = 206,25 est calculer au dessus)
Rappel de l'énoncé (avec le fichier joint):
Le moteur d'un monte-charge de type courant continu à excitation séparée est connecté à une tension de . La résistance de l'induit est de 0,08 ohm.
Le moteur monte une charge avec une vitesse v1 = 10 m/s (correspondant à une vitesse de rotation de 750 tr/min) en développant une puissance mécanique de 100 kw .
La figure ci-joint décrit le schéma de fonctionnement de l'excitation séparée.
Rd = (U / I1) - R induit = (500/206,25) - 0,08 = 2,34 ohm
A confirmer