Niveau école ingénieur

Exercice motard cascadeur

Posté par
Proxyness 02-01-18 à 11:33

Bonjour,

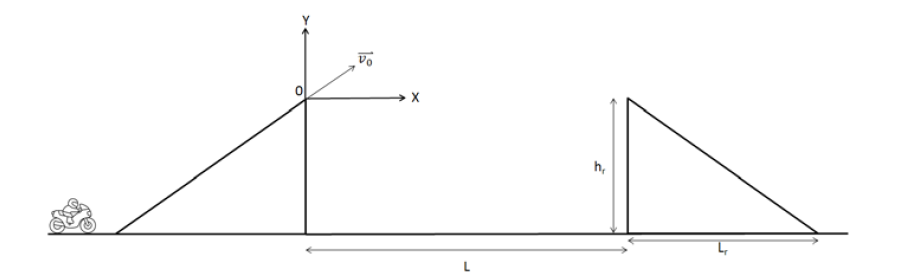
Je dois calculer la vitesse que le motard doit avoir au sommet de la première rampe pour réussir à atterrir sur la deuxième.
J'ai donc
$\vec{r}$ ₀ = $\begin{pmatrix} 0\\ 0 \end{pmatrix}$
a (t) =   $\begin{pmatrix} 0\\ -g \end{pmatrix}$
Et pour le vecteur vitesse, j'ai en fait calculer l'angle de la pente en faisant arctan (hr/Lr) = puis j'ai posé   $\vec{v}$ ₀= $\begin{pmatrix} v0 * cos \alpha \\ v0 * sin \alpha \end{pmatrix}$

Mais dans le corrigé, il est écrit:
$\vec{v}$ ₀= v₀* $\begin{pmatrix} Lr\\ hr \end{pmatrix}$ * (Lr² + hr²)^(1/2)
Du coup je me demandais si ce que j'avais fait est correct ou non et également, comprendre comment ils ont trouvé ceci.

Merci beaucoup d'avance!!

Exercice motard cascadeur

Posté par re : Exercice motard cascadeur 02-01-18 à 12:45

Hello

Si on suppose les 2 rampes identiques

$cos\alpha = \frac{L_r}{\sqrt{L_r^2+h_r^2}}$
$sin\alpha = \frac{h_r}{\sqrt{L_r^2+h_r^2}}$

Donc à la coquille prés du "*" qui doit être un "/", vous dites la même chose

Posté par re : Exercice motard cascadeur 02-01-18 à 17:20

Ah mais oui bien sûr ! Merci !! (et oui c'est bien juste, c'est moi qui ai oublié le signe moins à la puissance 1/2)

Du coup (pour éviter de trop me perdre ensuite en corrigeant, j'ai gardé leur façon d'écrire) j'ai
$\vec{v}(t) = \begin{pmatrix} vo * Lr (Lr^2Hr^2)^(-1/2) \\ -g*t + v0 * hr (Lr^2 + hr^2) ^(-1/2) \end{pmatrix}$

et
$\vec{r}(t) = \begin{pmatrix} vo * Lr (Lr^2Hr^2)^(-1/2) *t \\ -(g*t^2)/2 + v0 * hr (Lr^2 + hr^2) ^(-1/2) * t \end{pmatrix}$
(Les (-1/2) étant des puissances, je n'ai pas réussi à les mettre au dessus ensemble ... )

Pour trouver v₀, je ne suis vraiment pas sûre de ce que je fais, mais j'ai isolé le t de la première coordonnée de $\vec{r}$ (t), pour ensuite remplacer les t de la deuxième coordonnée de $\vec{r}$ (t).
Mais je n'obtiens pas vraiment la même chose que dans le correctif. Du coup j'imagine que ma démarche est fausse. Est-ce que vous auriez des pistes de ce que je dois faire ?

De plus, il fallait prendre en compte un temps T pour lequel $\vec{r}(T) = \begin{pmatrix} L\\ 0 \end{pmatrix}$ . J'ai bien compris la démarche là derrière mais par contre je ne sais pas quoi en faire ensuite. L'intégrer à une coordonnée?

Encore merci =)

Posté par re : Exercice motard cascadeur 02-01-18 à 19:13

Moi, j'aurais conservé les sinus et cosinus le plus longtemps possible. Et j'aurais résolu le problème en éliminant la variable temps

l'équation cartésienne de la trajectoire est

$y = -\frac{g}{2v_0^2cos^2\alpha}x^2 + tg\alpha x$

Et la 2eme rampe a pour équation:

$y = tg\alpha(L + L_r -x)$

Il te faut alors déterminer sous quelle condition sur v_0 la parabole et la droite ont une intersection comprise entre L et L+L_r

Il te faut pour cela étudier une équation du 2nd degré en x. Fastcohe?

Au fait, en Latex les exposants c'est ^{}

Posté par re : Exercice motard cascadeur 02-01-18 à 19:27

J'ai fait autrement (sans l'équation de la trajectoire y = f(x)) qui, je pense, alourdit les calculs.

En conservant (avec le repère dessiné) les équations paramétriques x(t) et y(t) du motard (supposé ponctuel).

En imposant une fois x = L et la condition y > 0
et une seconde fois en imposant y = -h et la condition x < L+Lr

et on arrive assez facilement à :

$\sqrt{\frac{g.L(h^2+L_r^2)}{2h.L_r}} < Vo < (L+L_r).\sqrt{\frac{g.(h^2+L_r^2)}{2h.L_r.(L+2.L_r)}$

Pas vérifié ...

Posté par re : Exercice motard cascadeur 03-01-18 à 11:13

Merci de vos réponses!

J'aurais également conservé les cos et sin en temps normal, je trouve que ça allège, mais c'est pour voir plus facilement si j'ai fait juste ou non avec le correctif, vu qu'il ne les utilise pas.

Désolée d'avance de ne pas tout réussir alors que ça a l'air enfantin. Avant ce semestre je n'avais plus fait de sciences dures depuis 4 ans du coup j'ai plein de lacunes que je comble au fil des exercices =$

Dirac: (merci pour l'astuce Latex!) comment as tu trouvé l'équation de la parabole? j'ai regardé comment faire sur internet mais je me retrouve toujours avec plus d'inconnus que d'équations et du coup je n'arrive à rien
Ensuite j'ai repris tes données pour voir si j'arrivais à le faire quand même, et une fois que j'ai obtenu x, est ce que j'ai le droit de reprendre l'équation de la parabole pour trouver v0 (je ne sais pas si c'est autorisé vu qu'on reprend la même équation)?

J-P: ton terme le plus petit est celui mis par le prof. Je voulais presque faire ça justement, appliquer comme condition x = L et y = 0, mais je ne sais pas ce que ça veut dire mathématiquement, c'est à dire comment l'appliquer sur mes termes. Est-ce que je prends les coordonnées de la position et je résous : v₀ * L_r* (L_r² + h_r² ) $^{-1/2}$ *t = L
et - $\frac{g*t^2}{2}$ + v₀ *h_r * (L_r² + h_r² ) $^{-1/2}$ *t = 0 ?

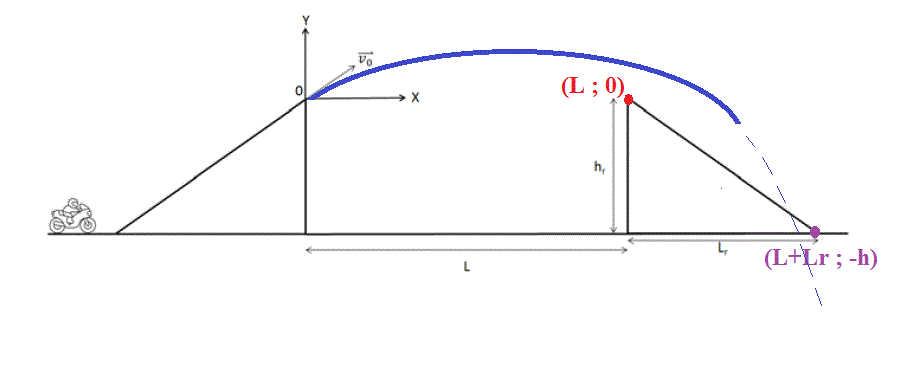
Posté par re : Exercice motard cascadeur 03-01-18 à 11:47

Exercice motard cascadeur

1°)

Il faut que le projectile passe au dessus du point de coordonnée (L;0) (en rouge sur mon dessin)

On a :
x(t) = Vo.cos(alpha)*t
y(t) = Vo.sin(alpha)*t - gt²/2

Pour y = 0 (et t différent de 0), il faut que x > L

y(t1) = 0 ( et t1 diff de 0) donne : Vo.sin(alpha) = gt1/2
t1 = 2Vo/g * sin(alpha)

Et il faut que x(t1) > L

Vo.cos(alpha)*t1 > L

Vo.cos(alpha)*2Vo/g * sin(alpha) > L

2 Vo².cos(alpha) * sin(alpha) > gL

Vo² > gL/(2sin(alpha).cos(alpha))

Or cos(alpha) = Lr/RCarrée(Lr²+h²) et sin(alpha) = h/RCarrée(Lr²+h²)

Vo² > gL/(2h/RCarrée(Lr²+h²) * Lr/RCarrée(Lr²+h²))

Vo² > gL*(Lr²+h²)/(2h.Lr)

Vo > Rcarrée[gL*(Lr²+h²)/(2h.Lr)]

Rcarrée[gL*(Lr²+h²)/(2h.Lr)] < Vo
------------
2°)

Et presque pareil pour le bas de la piste.

On cherche t2 pour que x(t2) = L+Lr

Et on en déduit y(t2) ... qui doit être < -h

Cela conduit à Vo < ...

------
Sauf distraction.
Exercice motard cascadeur

Posté par re : Exercice motard cascadeur 19-01-18 à 12:03

Désolée pour la lenteur de la réponse.

Je vois, merci beaucoup !! Ca m'a beaucoup aidé =)

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Exercice motard cascadeur

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique