Bonjour Astre21,

Le calcul n'est pas très difficile et à la portée d'un élève ingénieur, à mon avis. De plus, le résultat final est d'une simplicité enfantine, et très facile à interpréter, tu vas le voir :

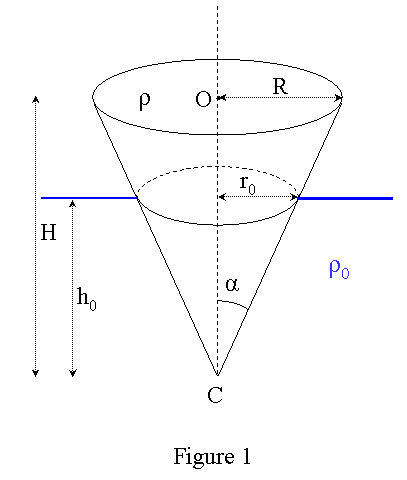
La première étape est la détermination de la profondeur d'immersion du cône, que j'ai appelée h₀ sur la figure 1 ci-dessous. Avec les notations de cette figure, le volume total du cône est V = πR²H/3, et celui de la partie immergée est V₀ = πr₀².h₀/3. Le poids du cône est Mg = ρVg (je préfère ρ plutôt que μ), la poussée d'Archimède est en norme A = ρ₀.V₀.g (ρ₀ est la masse volumique de l'eau) et l'équilibre est fourni par Mg = A, ce qui donne r₀².h₀ = R²H.ρ/ρ₀ ; en appelant α le demi angle au sommet du cône et en écrivant tanα = r₀/h₀ = R/H, on arrive à la relation h₀³ = H³.ρ / ρ₀.
Remarque : on pouvait arriver plus vite à ce résultat en écrivant que l'équilibre du cône partiellement immergé est donné par ρ₀.V₀ = ρ.V soit V₀/V = ρ / ρ₀,  en utilisant le rapport d'homothétie des deux cônes k = h₀/H et en écrivant V₀/V = k³ (relation vue en troisième et au programme du DNB).

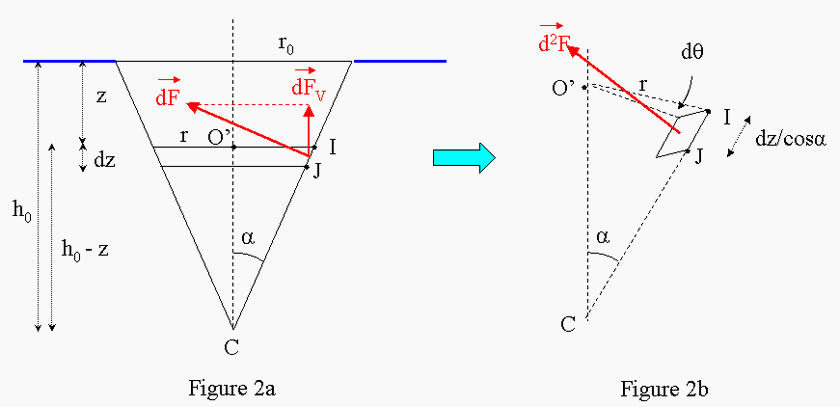
La deuxième étape consiste à calculer la résultante des forces pressantes qui agissent sur la partie du cône immergée dans l'eau, c'est-à-dire le long de la profondeur d'immersion h₀. regarde les figures 2a et 2b :
On découpe le cône en tranches d'épaisseur dz, situées à la profondeur d'immersion z, et chaque tranche est subdivisée en petites surfaces de dimensions r.dθ et IJ = dz/cosα, où r est le rayon du cercle constituant la tranche considérée. La force pressante agissant sur cette surface élémentaire est , en norme, d²F = p(z). (rdθ).IJ, où p(z) est la pression régnant à la profondeur z. Il est clair qu'il faut projeter d²F sur la verticale car ses composantes horizontales s'annulent deux à deux ; or l'angle entre d²F et la verticale vaut π/2 - α ce qui donne, lorsqu'on a fait un tour complet (θ variant de 0 à 2π, voir figure 2b), dF_V = p(z).2πr.IJ.cos(π/2 - α) et, avec IJ = dz/cosα, conduit à dF_V = 2πr.p(z).tanα.dz.

Il n'est pas nécessaire de tenir compte de la pression atmosphérique Patm, car elle intervient à la fois dans la pression p(z) à la profondeur d'immersion z et aussi sur la base du cône (surface de rayon R). Avec cette simplification, p(z) est simplement la pression manométrique ρ₀gz. ; on arrive donc à la relation dF_V = 2πρ₀.g.z.r.tanα.dz.  OK ? C'était le point le moins immédiat de ce calcul.

On va bien sûr intégrer selon la variable z, et il est temps de remarquer que r dépend de z par la relation r = (h₀ - z).tanα. Soit dF_V = 2πρ₀.g.tan²α.(h₀ - z).z.dz. L'intégration est menée depuis z = 0 jusque z = h₀. Le reste du calcul ne devrait alors plus poser de problème pour toi : on obtient F_V = π.ρ₀.g.tan²α.h₀³/3.

Or, avec la relation donnant h₀ (voir plus haut) et sachant que tanα = R/H, on obtient sans difficulté F_V = (πρgR²H)/3 = ρ.V.g, soit F_V =Mg : la résultante des forces pressantes, qui est verticale, compense donc le poids du cône, ce qui est plein de bon sens puisque le cône est immobile à la profondeur d'immersion h₀.
Pour t'en convaincre, tu peux reprendre cet exercice en remplaçant le cône par un cylindre de rayon R et de hauteur H. Le calcul est immédiat car il n'y a plus d'intégration à faire, et tu retrouveras le fait que la force pressante agissant sur le fond du cylindre compense exactement son poids.

Si tu as des questions n'hésite pas.

Prbebo.

Merci grace a ton explication j'ai compris. J'avais deja deviné le resultat final comme il etait preciser que le cone etait a l'equilibre.
Encore merci !

Eh bien tant mieux, car en relisant mon post je me rends compte que ce calcul est tout de même plutôt long, et pas si immédiat que ça.
Juste une remarque
: il n'est pas nécessaire que le cône soit dans cette position pour retrouver l'égalité entre le poids et la résultante des forces pressantes ; si on leste convenablement la base (face circulaire de rayon R), le cône flottera avec la pointe en haut. Dans ce cas, la résultante des forces pressantes agissant sur la face latérale sera dirigée vers le bas, mais il faudra lui "additionner" la force agissant sur la base (R².p(z) ) qui, elle, est dirigée vers le haut et qui va l'emporter sur la précédente. Le résultat donnera alors une force ascendante dont la norme sera égale au poids du cône, + celui de la surcharge.
Pourquoi ne pas essayer de traiter ce cas de figure, en attendant tes partiels ?
NB : la surcharge a pour but d'abaisser le centre de masse du cône, pour l'obliger à se maintenir dans l'eau "pointe en l'air".

B.B.