Inscription / Connexion Nouveau Sujet
Exercice électrocinetique Circuit RLC parallele
Bonjour , je bute sur cet exercice .
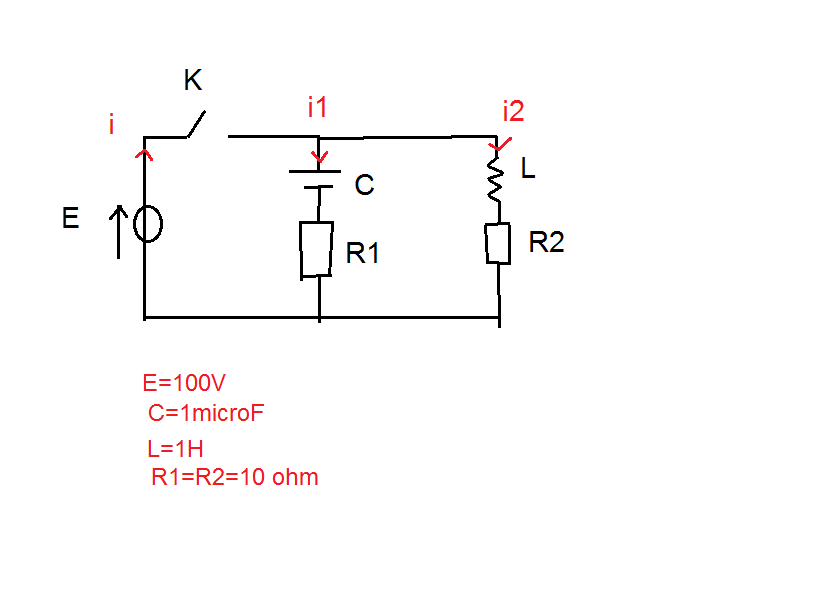
Alors voila on donne le circuit ci dessous .
On a àt=o i2(0)=0 et le condensateur est dechargé a t=0 , on ferme K
1)Determiner i1(t) et i2(t) , les representer graphiquement .
2)A quel instant a t on i1=i2
3)Apres un temps tres grand devant les constantes de temps RC et R/L on ouvre K , que se passe t'il ?
1)Je fais ma loi des noeuds i=i1+i2 avec i1=C*duc/dt+E/R1
Ul=L*di2/dt
E-Ri-Ul=0
E-R(i1+i2)-Ldi2/dt=0
E-R(C*duc/dt+E/R1+i2)-Ldi2/dt=0
E-R(LCd²i/dt²+E/R1+i2)-Ldi2/dt=0
je bloque a partir d'ici ( si toutefois mon equa diff est juste jusque la)
Je crois devoir passer en forme canonique puis calculer le discriminant sauf qu'avec cette equa diff c'est compliqué .)
2) ?
3)avec t> C completement chargé on peut le remplacer par un interrupteur ouvert
C completement chargé on peut le remplacer par un interrupteur ouvert
Besoin d'un peu d'aide SVP
Cordialement
Bonsoir,
Pourquoi utiliser la loi des noeuds ?
Il y a un circuit RC et un circuit RL qui ont chacun une tension constante E à leurs bornes. Ils peuvent être traités indépendamment.
Merci d'avoir repondu .
Donc si j'ai bien compris, j'etablis d'un coté mon equa diff du circuit RC puis de l'autre celle du circuit RL puis je rassemble tout ca .
En ce qui concerne la methode faut il comme dit precedemment calculer le discrminant de l'equation obtenue etc .. ou il faut utiliser une tout autre methode ?
Cordialement
Il n'y aura pas de discriminant.
Les équations différentielles seront du premier ordre.
Il ne faut pas "rassembler" tout ça. Tu calcules i1(t) et i2(t) en résolvant deux équations différentielles du premier ordre différentes.
Je suppose que tu sais le faire... sinon je t'expliquerai comment faire. Mais c'est du niveau terminale S, enfin ça dépend comment on résout l'équation différentielle.
d'accord . Etant donné que la bobine et le condensateur sont branchés en derivation c'est comme si on avait un circuit RC et un circuit RL alors que si bobine et condensateur etaient en serie on aurait un circuit RLC d'ou les deux equations du premier ordre si j'ai bien compris . C'est ca ?
J'etablit donc mes deux equa diff:
E=Ur1(t)+Uc(t)
Ur(t)=RCdUc(t)/dt
E=RCdUc(t)/dt+Uc(t)
dUc(t)/dt+Uc(t)/RC=E/RC
dUc(t)/dt+Uc(t)/tau=E/tau avec tau=RC
Solution: K*exp(-t/tau)+E=Uc(t)
Etant donné que C est dechargé: Uc(t)=E(1-exp-t/tau)
ET
E=Ur(t)+Ul(t)
Ul(t)=Ldi/dt et Ur(t)=R*i(t)
E=R*i(t)+Ldi/dt
E/L=R/L*i(t)+di/dt
di(t)/dt+i(t)/tau=E/L avec tau= L/R
Solution i(t)=Kexp(-t/tau)+E/R
i2(0)=0 i2(t)=E/R(1-exp-t/tau)
J'ai donc mes deux equations , comment je fais maintenant ?
Tu as bien compris...
On demande i1(t) donc
Donc
OK pour
Ensuite "A quel instant a-t-on i1 = i2 ? "
Eh bien, il suffit de faire .
Donc :
pour trouver t
i1(t)=C*dUc(t)/dt ou i1(t)=C*dUc(t)/dt+Uc(t)/R ?
Je comprends pas pourquoi tu ne fais pas apparaitre Uc(t)/R .
D'accord pour les deux solutions . Determiner sous entend faire l'application numerique ou se contenter des expressions literrales ?
Je me debrouille pour les representations graphiques.
Pour i1(t)=i2(t) je trouve t= 9.9*10^4 s ce qui est probablement faux.
je peux detailler mon calcul pour voir ou est l'erreur.
Déjà, il y a une petite inexactitude dans mes réponses :
Uc(t)/R n'a rien à faire là. i1(t) est égal à ou à
mais pas à un mélange bizarre des deux... ( UR1 = E - UC(t) ).
je peux detailler mon calcul pour voir ou est l'erreur.
OK, j'attends le calcul.
Alors je pars de
E/R exp(-t/RC=E/Rexp(-t/L/R)
exp(-t/RC)=exp(-t/L/R)
ln exp(-t/RC)=ln exp(-t/L/R)
-t/RC=-t/L/R
t(R/L - 1/RC)=0
t=1/RC-R/L
En effet , grosse erreure.
En effectuant le calcul avec la bonne expression j'ai encore un temps tres grand ( 10^4 )
La bonne réponse, avec les valeurs données, est 72,4 µs.
Mais comment fais-tu pour résoudre cette équation ?
pour trouvé un temps tres grand jusque la j'ai fait ca sauf qu'apres
-t/RC=ln(1)-ln exp(-R/L*t) c'est pas juste car on a pas ln(a*b)=ln a * ln b
Ca peut paraitre vraiment con de ne pas savoir resoudre une equation de ce type mais bon ..
On n'a pas ln(a+b) = ln a + ln b mais ln(ab) = ln a + ln b
Ce n'est pas "con" de ne pas savoir résoudre une telle équation car, à ma connaissance, on ne peut pas résoudre analytiquement une telle équation (enfin, a priori, je ne sais pas le faire...).
Cela se résout, à mon avis, avec le théorème du point fixe par exemple.
On ne peut le résoudre que numériquement.
Si tu remplaces t par 72,4 µs, tu verras que tu obtiens l'égalité.
On pourrait la résoudre facilement si les deux constantes de temps étaient égales mais ce n'est pas le cas.
Je pars de la valeur du point d'intersection de i1(t) et de i2(t)sur le graphique.
Et par approximations successives, je trouve une valeur la plus approchée possible.
Pour la 3, le temps étant long devant les constantes de temps, le condensateur est chargé à la tension max et le courant i2 est maximum également.
Lorsqu'on ouvre l'interrupteur, on a un circuit RLC avec les conditions initiales :
i1(0) = 0
Uc(0) = E
i2(0) = E/R
Il peut y avoir une décharge oscillante amortie ou non, selon les valeurs de R, L, C (R = R1+R2).
On obtient une équation différentielle du second ordre et on tombe sur le calcul d'un discriminant.
Si  > 0, pas de décharge oscillante.
> 0, pas de décharge oscillante.
Si  < 0, décharge oscillante amortie.
< 0, décharge oscillante amortie.
Si  = 0, on est à la limite des deux cas précédents (on appelle souvent ça le régime apériodique critique).
= 0, on est à la limite des deux cas précédents (on appelle souvent ça le régime apériodique critique).
En fait, il y a oscillation si la résistance est suffisamment faible.
Mais la question 3 est très vague et il est difficile de savoir ce qui est attendu.
On peut faire un grand développement sur cette question...
A part ça, je ne comprends pas l'intérêt de la question 2, surtout qu'on ne peut pas obtenir de réponse de façon analytique (enfin, à mon avis, s'il y a quelque chose que je n'ai pas vu et qu'il y a une solution analytique, tu voudras bien me le faire savoir mais ça m'étonnerait... ).
).


