Inscription / Connexion Nouveau Sujet
Exercice dynamique du mouvement rectiligne
Bonjour,
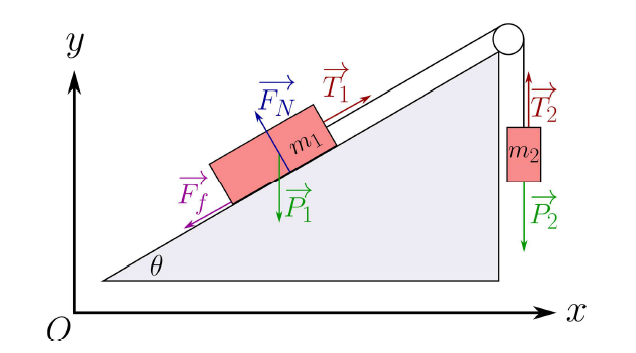
Je dois trouver l'expression algébrique de l'accélération d'un traîneau de masse 𝑚1, relié à un objet de masse 𝑚2 via un câble et une poulie de masse négligeable. Il est initialement au repos mais se met à bouger sous l'effet de la gravité à t=0. On doit également prendre en compte le frottement statique et dynamique du traîneau.
J'ai tout d'abord représenté mes forces sur un schéma puis poser toutes les coordonnées:
P1 =
P2=
Ff =
J'ai ensuite poser: F = m1*cos
F = m1*cos - Ff*cos
- Ff*cos  = m1 * a
= m1 * a
et  F = -m2g + m1*sin
F = -m2g + m1*sin - Ff * sin
- Ff * sin =m1 * a
=m1 * a
Ensuite j'ai voulu isoler le a, mais je ne trouve pas du tout la même réponse que dans le correctif ( ils ont a(t) = g * (m2 - m1* (sin  +
+  c *cos
c *cos  ) /(m2 + m1) ) et je ne vois pas du tout comment ils l'ont trouvé.
) /(m2 + m1) ) et je ne vois pas du tout comment ils l'ont trouvé.
J'ai également une deuxième question sur cet exercice. Plus tard il nous demande quelles sont les conditions pour que m2 soit à l'équilibre.
J'ai donc fait une  F = 0
F = 0  m1* cos
m1* cos
 m1 *
m1 *  s* cos
s* cos  mais dans le correctif c'est m1* sin
mais dans le correctif c'est m1* sin
 m1 *
m1 *  s* cos
s* cos et je n'arrive pas à voir pourquoi?
et je n'arrive pas à voir pourquoi?
Merci beaucoup d'avance de m'avoir lue et de m'aider =)
Bonjour,
Avant d'écrire le pfd il faudrait que tu précises le(s) système(s) considéré(s), ainsi que le référentiel et le repère utilises pour l etude
Bonjour,
Merci de ta réponse. Que veut dire pfd ? C'est les coordonnées des vecteurs?
Je considère le traineau et la masse, pour le repère j'ai utilisé le repère x, y du schéma et pour le référentiel le sol plat?
Pfd = principe fondamental de la dynamique
Le référentiel est le référentiel terrestre supposé galileen
tu considères le système constitué des masses m1 et m2 avec ou sans le câble ?
À quoi correspond a ?
Merci, du coup ça correspond à la somme des forces.
Je les considère séparément mais j'avoue que je ne sais pas si c'est juste vu que c'est en fait un tout.
Aaah oui! Je crois que je commence à comprendre. L'accélération correspond à l'accélération que prend la masse 1 à cause de son poids attiré par la gravité et en bravant les forces de frottements et le poids de m2 qui le retiennent ?
Par contre je ne vois pas pourquoi on prend la coordonnée y de p1 et p2 mais x pour  c.
c.
Je n'arrive pas à comprendre à quoi correspond m1 + m2 au dénominateur. Est ce que c'est pour faire une sorte de moyenne de la masse vu que l'accélération est liée au deux masses?
D'ailleurs je viens de faire attention au fait que le corrigé ne prends pas en compte le coefficient de frottement statique. Comme l'objet était initialement au repos, est ce qu'on ne devrait pas justement l'inclure dans notre donnée?
Ta projection de P1 dans (O,x,y) n'est pas bonne
S'il y a glissement c'est le frottement dynamique qu'il faut prendre
Quand je vois tes équations j'ai l'impression que tu as essaye d'appliquer le pfd au système constitué des 2 masses et du câble
Mais dans ce cas il y a une réaction au niveau de la poulie et surtout l'accélération est celle du centre de gravité du système qui est déformable, ce qui complique bcp les choses!
Ici il faut mieux isoler m1 puis m2 et appliquer le pfd à chacun de ces systèmes
Tu remarques que m1 et m2 ont même acceleration (en module) si le câble est inextensible
Et que T1 = T2 en module puisqu on néglige l'inertie du câble et de la poulie
En éliminant la tension des équations tu dois trouver a
Ah oui juste! Ca vaut =
D'accord je vois! Je ne le savais pas (qu'il fallait poser une somme des forces à chacun des éléments).
Du coup j'ai fait
-m1g - Ff sin =m1a
=m1a
-m2g - Ff sin =m2a
=m2a
je les ai sommé et ai obtenu
(g(-m1 -m2) - 2 Ffsin ) / (m1 +m2) =a
) / (m1 +m2) =a
Ff =  c * N
c * N
Par contre j'ai un doute pour N, c'est la force de réaction du sol envers l'objet, du coup c'est mais est ce que je dois prendre en compte qu'on est sur un sol ayant un angle
 ? Dans ce cas là, est ce qu'on a pour coordonnée y, m1g * cos
? Dans ce cas là, est ce qu'on a pour coordonnée y, m1g * cos .
.
J'ai mis en gras, les erreurs que j'ai encore, et que je ne vois pas d'où (le signe moins avant m2, le 2, et le sin, mais je sais pas s'il y aura une identité remarquable avec la force normale), il me manque aussi m1sin , est ce que c'est parce que le poids m1 doit monter une pente?
, est ce que c'est parce que le poids m1 doit monter une pente?
Encore merci de m'aider! J'y vois quand meme beaucoup plus clair!
Tu peux appliquer le pfd au système que tu veux mais il faut bien définir ce système
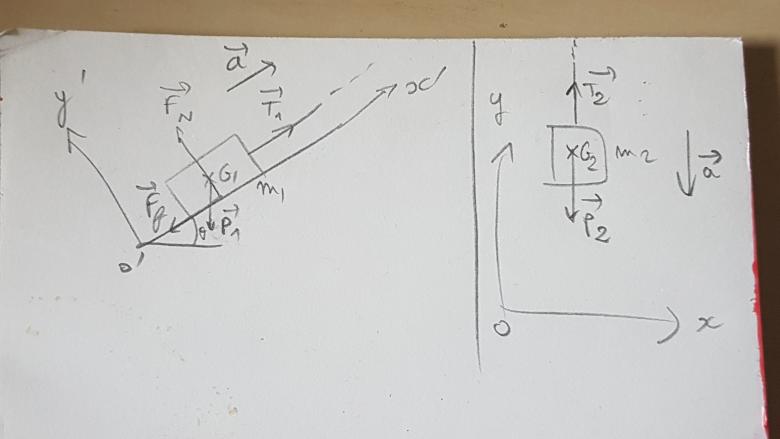
Ici on peut isoler m1 et m2 et appliquer le pfd à chacun des systèmes indépendamment
Cf croquis
Il faut bien définir ton système avant d'appliquer le pfd sinon tu mélangés tout...
Ici par ex. , m2 n'est soumis qu'à T2 et p2
si on l'isole
Ah! Du coup quand je prends 2 systèmes séparément je ne suis pas obligée de conserver le même repère ? Je ne savais pas du tout!
Donc je fais un schéma pour chacun d'eux et je réécris leurs coordonnées selon ce schéma puis la somme des forces pour chacun séparément, et ensuite j'ai le droit de les remettre directement en lien en sommant les deux sommes ou est ce qu'il y a un intermédiaire à faire?
Algebriquement tu combines les eq. comme tu veux
Et dans un referentiel donné, tu peux projeter dans le repère que tu veux ça ne doit pas changer le résultat physique
J'ai réussi!! merciii beaucoup!!Du coup j'ai également compris pour la deuxième question de l'exercice. Vous n'imaginez pas à quel point je suis contente =D
Petite question, du coup, quand je somme les 2 pfd, ça ne pose donc pas de problème que l'un des pfd soit sur les coordonnées x et l'autre y? J'avoue que j'ai du mal à comprendre comment ça se fait (même si je vois bien que du coup c'est bien ça).
En fait je crois avec compris! C'est parce qu'on a isolé le a, donc on prend les deux termes égaux à a, et que de toute manière peut importe x ou y, dans ce cas-ci l'accélération est identique pour p1 et p2 ?
Par contre je viens de me rendre compte que j'ai pas mis la force N dans mon pfd de p1 et je me demande si c'est juste (vu que j'arrive au même résultat). Et si oui, je ne suis pas sûre de comprendre. Est ce que c'est parce que dans ce cas là la force normale n'a aucune conséquence sur le mouvement de p1?
Erratum, j'aurais du tester avant de dire ça, ça ne fonctionne pas du tout en isolant a, du coup ça ne doit pas être ça. Désolée pour le triple message... =$
Le pfd est une relation vectorielle vraie dans tout repère (à condition d'être dans un ref.erentiel galileen)
Tu choisis un repère et tu projettes sur les axes
Tu obtiens alors des relations algébriques (= entre nombres)
Et ensuite le problème se résout de façon purement algébrique en combinant les relations comme en maths
(Peu importe de quelle projection elles pro viennent)
Ici pour { m1} tu obtiens 2 relations en projetant sur x' et y'
(Sur mon dessin) et FN n'intervient que dans une des relations
Tu en as besoin pour calculer Ff