Inscription / Connexion Nouveau Sujet
Exercice de physique sur champ et potentiels électriques
Bonjour,
J'ai un exercice de physique à rendre sur lequel je bloque complètement. Voici l'énoncé :
On considère un champ électrique extérieur uniforme dirigé suivant l'axe des x et vers les x>0.
1) Montrer en utilisant la relation E=-grad(V) que le potentiel électrique correspond au champ électrique E(extérieur) uniforme s'écrit Vext(x, y)= - ||Eext||x+V(o) où V(o) est le potentiel électrique au point O (x=0). Comment sont les équipotentielles ?
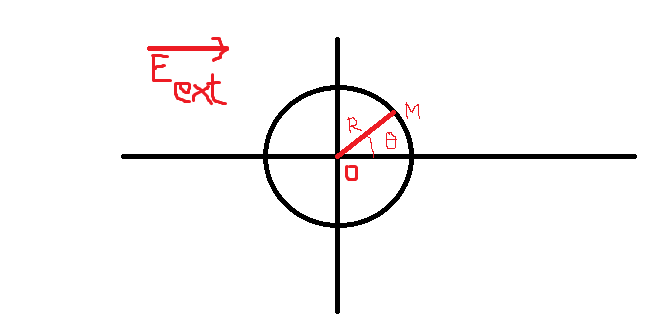
2) En déduire l'expression du potentiel extérieur Vext(M) pour un point M du cercle de centre O et de rayon R en fonction de R et têta (cf figure).
3) On place au centre du cercle un dipôle p orienté suivant l'axe (Ox) . Si têta est l'angle entre l'axe (Ox) et la direction (OM) et si r=||OM|| alors quand r>>d, le potentiel Vdipole au point M peut s'approcher par l'expression suivante : Vdipole(M) = (pcos(têta))/(4piεr^2) où p = ||p|| = qd est l'intensité du moment dipolaire.
En supposant l'approximation valable sur le cercle, déduire le potentiel total V = Vdipole + Vext en un point M du cercle en fonction de p, têta et R.
Merci beaucoup à ceux qui voudront m'apporter de l'aide car je ne vois pas du tout comment procéder...
Bonsoir
En projetant la relation entre le vecteur champ et le potentiel sur les trois axes tu obtiens :
Ensuite :
Je te laisse réfléchir à tout cela et proposer une solution.
Je ne comprends pas comment vous arrivez au fait que dV/dx = - ||Eext|| et que dV/dx = 0.
De plus, en écrivant x = R.cos(têta) vous considérez que x est l'abscisse du point M, mais je ne vois pas à quoi cela peut me servir... 
vanoise
Du moins je peux écrire pour la question 2 que
Vext(M) = - ||Eext||.cos(têta).R + v(O)
Mais cela est-il suffisant ? Puis-je retirer de mon équation le "+V(O)" ?
Les questions 2) et 3) sont sans grand intérêt physique...Il suffit de recopier des formules comme tu l'as fait pour la question 2. Elles sont là pour préparer d'autres questions très intéressantes ultérieures qui, apparemment ne sont pas posées pour l'instant... En revanche, la question 1) est très intéressante...
As-tu bien compris la définition du gradient ? Es-tu à l'aise avec la notion de dérivée partielle ? Si non : revois ton cours sur le sujet ; si oui, les trois expressions de dérivées partielles que je t'ai fournies à 19h26 devraient suffire à te permettre d'aboutir au résultat...
Réfléchis bien et poste à nouveau si vraiment tu ne t'en sors pas.


