Inscription / Connexion Nouveau Sujet
Exercice de mécaniques
Bonjour.
Je n'arrive pas à faire un exercice de mécanique.
L'énoncé du sujet est le suivant :
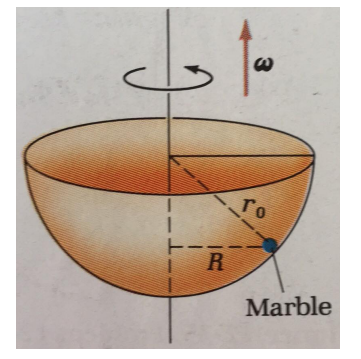
Soit un bol qui tourne avec un vitesse angulaire w.
On place une bille dans ce bol à une distance R de l'axe des ordonnées.
Cette bille reste à cette position tout au long du mouvement.
Montrer que R = SQRT(ro²-(g/w²)²)
Merci
Bonjour
Lorsque la bille est immobile par rapport au bol, elle est animée par rapport à la terre (référentiel galiléen) d'un mouvement circulaire uniforme de rayon R et de vitesse angulaire  . Tu peux déterminer les caractéristique de son vecteur accélération par rapport à la terre (accélération normale centripète). Il te suffit alors d'appliquer la relation fondamentale de la dynamique à la bille sachant que celle-ci est soumise à deux forces :
. Tu peux déterminer les caractéristique de son vecteur accélération par rapport à la terre (accélération normale centripète). Il te suffit alors d'appliquer la relation fondamentale de la dynamique à la bille sachant que celle-ci est soumise à deux forces :
son poids
la réaction du bol que l'on peut, en absence de frottement, considérer comme orientée vers le centre du bol (selon le segment pointillé notée ro)...
Commence par faire un schéma propre où tu représenteras les divers vecteurs utiles...
Tu pourras répondre après avoir considéré que la bille est soumise à son poids et à la force centrifuge due au mouvement de rotation du bol, et que la bille prend une hauteur au-dessus du fond du bol telle que la somme de ces deux forces soit normale à la surface du bol là où se trouve la bille.
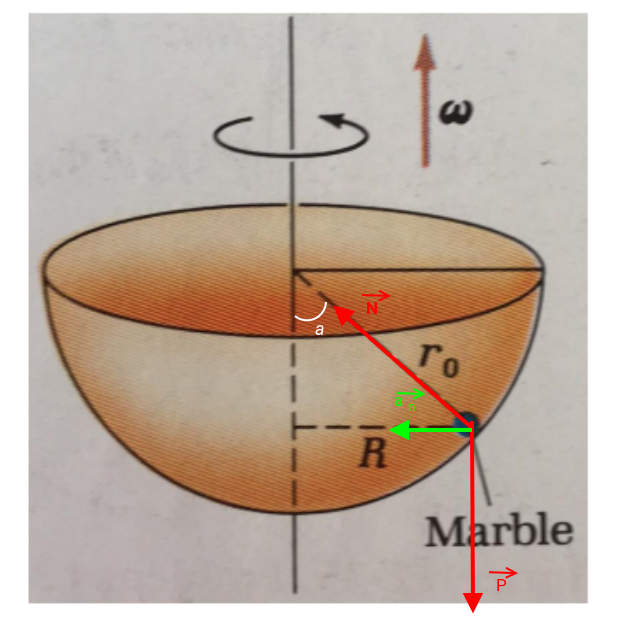
Pour t'aider un peu, voici le schéma complété correspondant au raisonnement effectué dans le repère terrestre supposé galiléen. La bille est bien soumise à deux forces : son poids de vecteur et la réaction normale du bol de vecteur
. Son accélération par rapport à la terre est normale centripète, de vecteur
Il existe une autre méthode consistant à étudier l'équilibre dans un repère lié au bol. Ce repère n'étant pas galiléen, il y a lieu d'ajouter aux deux forces réelles un terme correctif appelée force d'inertie centrifuge. Les deux méthodes conduisent au même résultat.
Merci pour votre aide.
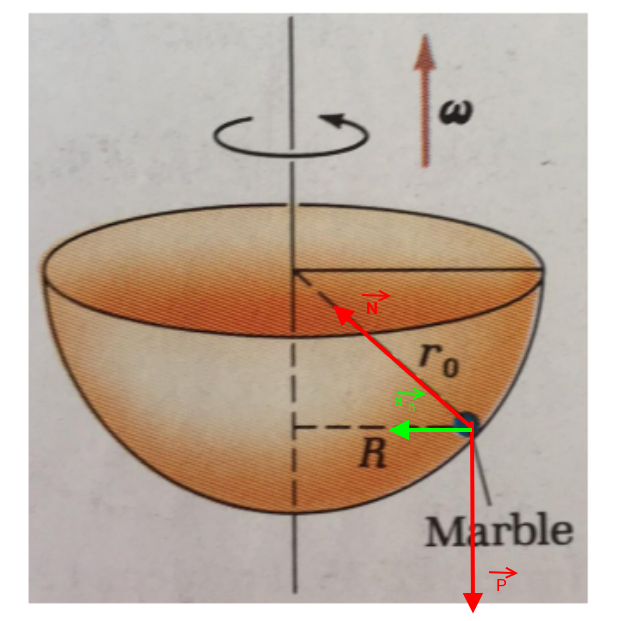
Après avoir trouver les vecteurs, faut-il réaliser une projection sur un axe ?
Et comment faire pour trouver la valeur de N ?
Après avoir trouver les vecteurs, faut-il réaliser une projection sur un axe ?
Oui , ou plus exactement, sur deux axes : un horizontal et un vertical ; je te laisse le faire ; tu devrais assez facilement arriver à démontrer :
Inutile de calculer la norme du vecteur N.
En exprimant ensuite tan(a) dans le triangle rectangle du schéma et en identifiant, on obtient le résultat. (Ne pas oublier Pythagore...)