Inscription / Connexion Nouveau Sujet
Exercice de mécanique
Je cherche à résoudre l'exercice suivant:
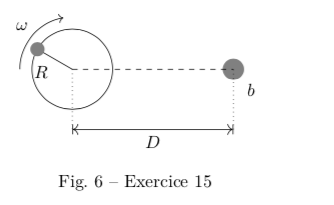
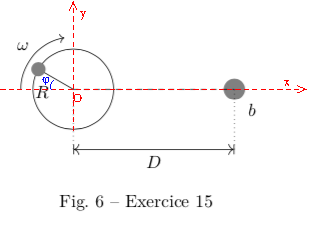
Une pierre attachée à une fronde tourne à la vitesse angulaire ω. La pierre doit atteindre un poteau b qui se trouve à une distance D du centre du cercle de rayon R. En quel point doit-on lâcher la pierre?
J'ai un peu de mal avec l'intuition physique pour résoudre ce genre de question.
Je dois trouver, d'après le correctif, trouver que ce point est , mais je ne vois pas la justification géométrique.
Merci pour l'aide d'avance!
Bonjour
J'imagine que, pour obtenir quelque chose d'aussi simple, il existe une relation entre 
et g...
Que représente exactement l'angle 
? (origine des abscisses angulaires ?)
Définir un angle à partir d'un cosinus est incomplet car cos()=cos(-)...
Bref : un énoncé complet serait le bienvenu. D'autre part : pourrais-tu expliquer ce que tu as réussi à faire et ce qui te bloque ? Il serait plus facile de t'aider ensuite...
Bonjour,
Merci pour votre réponse!
J'ai vraiment mis l'entièreté de l'énonce, tel quel!
Je bloque effectivement sur la compréhension du type de réponse qu'on attend, puisque je suis bien d'accord que la définition de phi est floue.
Je ne suis pas parvenue à faire grand chose, puisque j'ai d'abord tenté de jouer avec l'équation d'un tir parabolique (ce qui est vain et peu justifié) :/
Avec un tel énoncé, on ne peut être sûr de rien !
j'ai d'abord tenté de jouer avec l'équation d'un tir parabolique (ce qui est vain et peu justifié)
Puisqu'il s'agit d'une fronde, on peut penser que le mouvement se produit dans un plan vertical confondu avec le plan de figure, les frottements étant négligés. Je ne voit pas ce qui est "vain et peu justifié" d'essayer dans ces conditions d'établir l'équation de la trajectoire dans un repère d'origine O. En choisissant convenablement l'origine des angles polaires, on peut poser :
xo=-R.cos(
) ; yo=R.sin()
vox=R.
.sin() ; voy=R..cos().
Tu peux alors rechercher les conditions pour que la trajectoire passe par le point de coordonnées (D,0). Dans le cas général, le résultat n'est pas très simple et fait intervenir g et R.
, ce qui paraît assez intuitif : plus R. est grand, plus la vitesse initiale est élevée, plus le tir doit être "en cloche" ; une vitesse angulaire très faible ne permet pas d'attendre la cible quel que soit l'angle de tir, une vitesse initiale assez élevée suppose un tir plus tendu...
Tous ces fait expérimentaux simples sont en contradiction avec ta correction...
Je voulais dire vain dans la mesure où je ne voyais comment aboutir à quelque chose! Mais avec vos indications, je vais ressayer d'en tirer quelque chose 
Merci beaucoup
Pour arriver au résultat simple de ton corrigé, on peut faire une hypothèse simplificatrice : il suffit de poser : R2>>g. Dans ces conditions, l'influence de la pesanteur est négligeable ; la vitesse du projectile en quittant la fronde est tellement grande que la portion de parabole correspondant à la trajectoire est assimilable à un segment de droite dirigée par la vitesse du projectile quittant la fronde.
Annuler
connectez vous