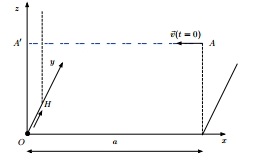
Énoncé : Un homme H se déplace sur une droite horizontale Oy d'un mouvement uniforme de vitesse v.. A t=0, il est au point O et dirige son minidrone D, alors au point A, de manière à ce qu'il puisse le surplomber à la verticale (soit le point A' à t=0), cf. figure. On admettra que le minidrone vole dans un plan parallèle (A'xy) au sol, y possédant une vitesse constante double de celle de l'homme et constamment orientée vers la verticale passant par l'homme.
Trouver la courbe décrite par le minidrone et le temps qu'il mettra pour surplomber son propriétaire.

Indications : après avoir exprimé une contrainte d'ordre géométrique, il sera utile d'introduire la distance l parcourue par le drone en fonction du temps puis (dl)². Enfin, la résolution de l'équation différentielle nécessitera le passage par un changement de variable tel que dy/dx = u = sinh (phi)...

La solution est : (y-(2a/3))² = ax((x/3a)-1)².

Pour l'instant, après une multitude de fausses pistes, j'en suis à :

Petite variation entre l'instant t et l'instant t+dt.
J'ai réalisé un triangle  selon A(t), A(t+dt) et la parallèle à Ox.
L'angle est l'angle entre la parallèle à Ox et le vecteur A(t)A(t+dt).

Selon ce triangle rectangle, je pose son hypoténuse dl, son côté opposé dy et son côté adjacent dx. Ce qui me donne (dl)²=(dy)²+(dx)².

Je me retrouve alors avec (dl/dx)²=1+(dy/dx)².

Mais je n'aboutis pas. Quelqu'un pourrait-il me dire si ce que j'ai fait est juste ? Sinon, quelles seraient les autres pistes ?

Merci d'avance.