Bonjour et bienvenu
Peux tu scanner le schéma et préciser ce que tu es capable de faire. Plus facile de t'aider ensuite. Cherche du côté des formules de conjugaison du dioptre plan

Salut Merci pour ta réponse. L'exercice n'est pas venu avec de schémas. Je connais les formules de conjugaisons. Mais je n'arrive pas à schématiser la situation par ce que je comprend pas très bien le principe. Es ce que le support est une surface réfléchissante, absorbante ou un dioptre plan.

Bonjour
Pour les visées il faut utiliser les réflexion s partielles ou au besoin marquer les faces au feutre. L'épaisseur de la lame semble être z3 - z1 alors que l'image de la face inférieure de la lame (cote z3) par le dioptre plan de cote z1 est une image  virtuelle de cote z2.

salut ,
j'ai pas tout fait ( parce que après kho-lanta , je suis un peu fatigué ! ) mais c'est un début de réponse çà pourra te lancer . j'écris pas toute la démo si tu n'y arrives pas je t'expliquerai mais en principe tu vas y arriver .
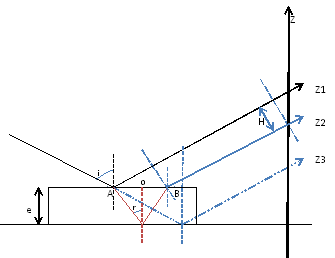
Moi, je trouve Z1Z3 = 2e et Z1Z2 = (2e/n)*(cos i/cos r)
normalement comme y'a pas de condition sur i le rapport est constant , en gros , tu peux choisir l'angle d'incidence i que tu veux çà marche.

Bonjour
Effectivement  Kho  lanta n'a pas que des effets  positifs. Il faut se placer dans les conditions  de Gauss  et écrire que le dioptrie plan de cote  z1  donne  de l'objet  de cote z3  une image  de côté z2 . La distance  dioptrie -objet venant  d'être  déterminée,  la seule inconnue  est n. Il faut connaître la formule de conjugaison du dioptre plan  dans  les conditions  de Gauss ou au besoin la redemontrer

Salut , c'est vrai que la télé c'est pas très bon pour le cerveau... mais c'est bon pour le moral ) . Bon, condition de Gauss =  rayons peu inclinés et peu éloignés de l'axe optique et ici ... y'a pas d'axe optique , ce n'est pas un exercice sur les lentilles . les conditions de Gauss permettent d'éviter certaines aberrations des lentilles lorsqu'on s'éloigne ou que les rayons sont trop inclinés par rapport à l'axe optique.
Pour ma part pour résoudre l'exercice on se retrouve avec 2 équations et 2 inconnus (une grâce à Z1Z2 en fonction de n et e  et l'autre grâce à Z1Z3 en fonction également de n et e  ; il faut bien travailler sa trigo pour en arriver là)
Mais bon si t'as un petit schéma accompagné d'une petite démo pour expliciter ta vision (optique 2000 ! ) , ce serait sympa de nous faire partager , j'ai hâte de voir ce que tu vas nous proposer  

Resalut,
cela m'a intrigué tes histoires de dioptres plan , je suis parti faire un peu de surf  pour me rafraîchir la mémoire , effectivement on peut envisager l'exo avec Z2 image vituelle de Z3
dans ce cas on aurait Z1Z2=e(1-1/n ) mais mais je vois pas l'intérêt de faire la visée Z3...
pour info :  
Mais je reste sceptique ...sand23 c'est quoi le niveau de l'exo    Licence 1er a ou L3 ?

***Raccourci url ajouté***

Cet exercice est de niveau (bac +1) et constitue une application directe du cours sur les dioptres plans.  J'ai expliqué dès le début l'intérêt de z3 : la mesure de e. Connaissant e, la mesure de z2 permet la détermination de n...

salut ,
compris dans le principe mais je ne vois toujours pas comment se font les visées...surtout celle de Z3, quel point faut-il viser sur l'horizontal du support plan ? un petit schéma serait vraiment bien venu...

Bonjour,
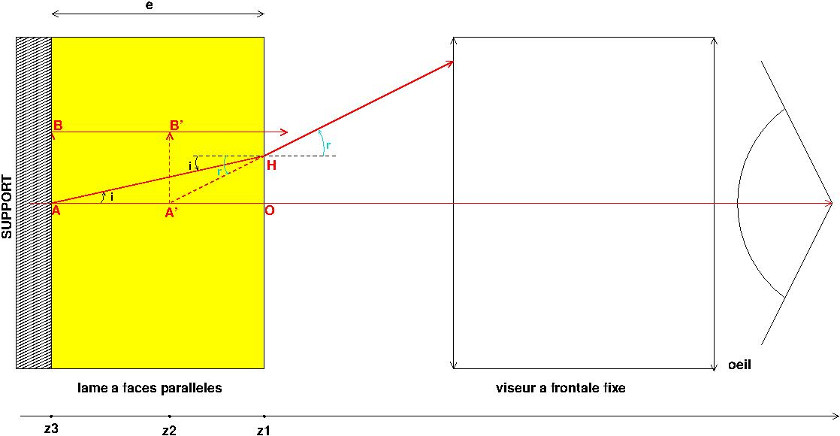
Le système ” adéquat ” de visée dont parle l'énoncé est sans doute un viseur à frontale fixe. C'est un viseur à travers lequel on ne peut ” voir ” distinctement que des objets plans perpendiculaires à son axe optique situés à une distance bien déterminée de la face avant du viseur, distance fixée par le constructeur. En pratique, on commence par enlever la lame et on place le viseur de façon à voir distinctement la paroi du support, ce qui permet de repérer sa cote z3. On place alors la lame. Celle-ci donne de la face précédente une image virtuelle décalée vers la droite. Il faut donc décaler d'autant le viseur vers la droite pour observer l'image de la paroi par le dioptre plan dont la cote est z2. Enfin on vise la face ” avant ” de la lame de cote z1. Cette visée est possible grâce aux inévitables grains de poussières présents sur la surface de la lame. On peut éventuellement tracer un trait au crayon feutre sur cette face. Je refais rapidement la démonstration concernant le dioptre plan. Soit un point A de la surface du support (cote z3) ; il se comporte comme un objet réel. Un rayon émis par A perpendiculaire à la lame ne subit pas de déviation. Conséquence : l'image A' de A, si elle existe, est sur la perpendiculaire à la lame passant par A.

Soit maintenant un rayon issu de A incliné de l'angle i par rapport à la perpendiculaire précédente. Il subit une réfraction sur le dioptre de cote z1 conformément aux lois de Descartes. Le prolongement du rayon réfracté coupe la perpendiculaire précédente en A'. Peut-on dire que A' est l'image virtuelle de A ? La réponse est ” oui ” seulement si tout rayon issu de A a son prolongement en A' après réfraction sur le dioptre plan. Cela est équivalent à dire que la position de A' ne doit pas dépendre de la valeur de l'angle i. Essayons de voir si la position de A' dépend ou non de la valeur de l'angle i. Les triangles rectangles (OHA) et (OHA') permettent d'écrire :





Soit en tenant compte de la loi de Descartes :   :


On constate que la position de A' dépend de l'angle i. Le dioptre plan ne constitue pas un système rigoureusement stigmatique : tout rayon issu de A n'a pas son prolongement passant par A'. En revanche, si on se limite à des rayons peu inclinés par rapport à la normale au dioptre, on peut poser : . Nous obtenons un stigmatisme approché en se limitant à des rayons peu inclinés par rapport à la normale au dioptre plan. Dans ces conditions, on peut écrire, au premier ordre près :



Remarque hors sujet dans le cadre de cet exercice : en remarquant qu'un rayon normal au dioptre issu du point B n'est pas dévié, on peut facilement montrer que le grandissement transversal du dioptre plan vaut +1.
Applications numériques :
épaisseur de la lame :



indice relatif de la lame par rapport à l'air :



(résultat fourni avec 4 chiffres significatifs compte tenu de la précision des données numériques.)
Remarque : Si cela intéresse quelqu'un, je veux bien expliquer le principe du viseur à frontale fixe... Evidemment, la figure fournie n'est pas à l'échelle...