Niveau maths spé

Exercice d'electrostatique : Polarisabilité

Posté par
Xardas45 23-10-16 à 01:07

Bonsoir, j'aurai besoin d'aide, voici l'énoncé :

Citation :
[sub][/sub]On se propode d'étudier une répartition surfacique de charge

0 * cos

avec

= (ex,OM) sur une sphere de rayon R ( ex est le vecteur unitaire horizontale ).
Pour etudier une telle distribution, nous allons d'abord montrer l'équivalence ci-contre :
Deux boules de rayon R, de centre O1 et O2, uniformément cargé en volume, l'un avec la densité volumique -

, l'augre avec la densité volumique +

, ont leur centre suivant Ox ( O est entre O1 et O2 ) et distants de a ( a << R ).
Ce type de distribution peut être obtenu suite à l'action d'un champ exterieur.

1 ) Montrer que cette distribution est équivalente à une distribution surfacique de type

0 * cos

2) En deduire le champs electrique à l'interieur de la boule. On pourra utiliser le principe de superposition.

3) Déterminer le champs electrostatique à l'exterieur de la boule chargée, et montrer au'il est équivalent à celui crée par une distribution dipolaire dont on calculera le moment p

Alors j'ai une petite correction pour la 1) : ils disent que dq =

*dV =

*M1M2 *dS et calculer M1M2 avec l'approximation :

0 =

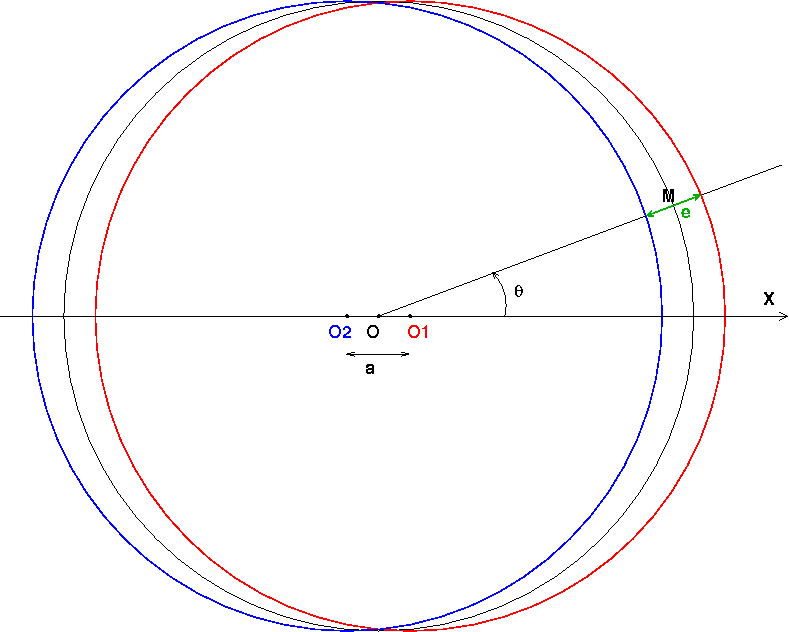
Posté par re : Exercice d'electrostatique : Polarisabilité 23-10-16 à 01:09

A noter que mes sont en fait des .

Merci d'avance

Posté par re : Exercice d'electrostatique : Polarisabilité 23-10-16 à 14:51

Bonjour
Le schéma ci-dessous devrait t'aider ; j'ai fortement exagéré la valeur de a pour plus de clarté mais il faut imaginer a<<R = OM.
Imagine la boule de centre O1 chargée avec la densité volumique et la boule de centre O2 chargée avec la densité volumique -. Tout l'espace commun aux deux boules est électriquement neutre. L'espace entre la boule "rouge" et la boule "bleue" a pour densité volumique de charge pour x>0 et pour densité volumique de charge - pour x<0.
Rigoureusement, une densité surfacique de charge, comme une distribution surfacique de masse en mécanique, cela n'existe pas ! Il s'agit seulement d'une distribution volumique lorsque l'épaisseur de la distribution est très faible devant les autres dimensions du problème. Imagine une surface élémentaire dS de la sphère de centre O et de rayon R, centrée en M : l'épaisseur e de matière chargée au voisinage de M est :
e = a.|cos()| ; le volume élémentaire de matière chargée autour de M est celui d'un cylindre de base d'aire dS et de hauteur e. Ce volume élémentaire contient la charge élémentaire :
dQ=.e.dS
Comme e <<R, on peut poser : dQ=.dS avec =.a=.a.|cos()|
Ce raisonnement fait pour un point M d'abscisse X>0 peut se généraliser à tout point M de la sphère compte tenu des remarques préliminaire sur le signe de :
=.a.cos(). On peut poser : _o=.a
Ces remarque simplifient fortement la suite du problème : tu as certainement appris à déterminer l'expression du vecteur champ électrique en un point quelconque d'une boule uniformément chargée. Ici, le vecteur champ électrique en un point quelconque est la somme du vecteur champ créé par la boule "rouge" et du vecteur champ créé par la boule "bleue"...

$Exercice d\'electrostatique : Polarisabilité$

Posté par re : Exercice d'electrostatique : Polarisabilité 23-10-16 à 20:56

Bonsoir, merci de ta réponse.

Il y a juste 2 choses que je ne comprends pas : comment ça se fait que e = a |cos()| et que l'on puisse prendre comme base du cylindre le dS de la boule, la base ne serait pas plane et ne pourrait pas formé une base de cylindre non ?

Posté par re : Exercice d'electrostatique : Polarisabilité 23-10-16 à 22:43

En toute rigueur, tu as raison : un élément de surface de la sphère est une calotte sphérique, pas un petit disque ! Cependant si l'élément de calotte sphérique est de très petite dimension par rapport au rayon de la sphère, on peut considérer cet élément de surface comme appartenant au plan tangent à la sphère en M. C'est un peu comme si, au bord de la mer par temps calme tu regardes la ligne d'horizon : en toute rigueur, il s'agit d'un arc de cercle : en pratique, comme tu ne peux en voir qu'une partie de longueur très inférieure au rayon terrestre, la portion visible de la ligne d'horizon peut être assimilée à un segment horizontal...
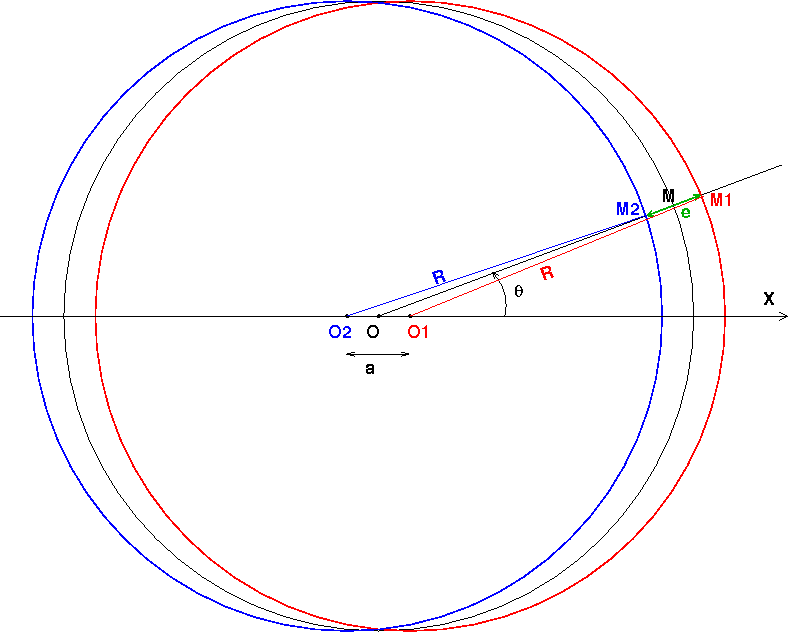
Pour l'expression de e, il faut écrire : $e=OM_{1}-OM_{2}$ puis calculer OM₂ et OM₁ par le théorème d'Al Kashi appliqué aux triangles OO₂M₂ puis OO₁M₁. Je fais le calcul pour le premier cas et te laisse faire le second.

$OM_{2}^{2}=OO_{2}^{2}+O_{2}M_{2}^{2}-2\cdot OO_{2}\cdot O_{2}M_{2}\cdot\cos\left(\theta\right)=\frac{a^{2}}{4}+R^{2}-a\cdot R\cdot\cos\left(\theta\right)$

$OM_{2}=R\cdot\left(1-\frac{a}{R}\cdot\cos\left(\theta\right)+\frac{a^{2}}{4R^{2}}\right)^{\frac{1}{2}}$

Puisque a<<R, il est possible d'effectuer un developpement de Taylor limité au premier ordre en $\frac{a}{R}$ .

$OM_{2}\approx R\cdot\left(1-\frac{a}{2R}\cdot\cos\left(\theta\right)\right)$

De la même façon on obtient : $OM_{1}\approx R\cdot\left(1+\frac{a}{2R}\cdot\cos\left(\theta\right)\right)$

Cela conduit bien à :

$e=OM_{1}-OM_{2}\approx a\cdot\cos\left(\theta\right)$

La démonstration a été faite dans le cas de la figure telle que $\cos\left(\theta\right)>0$

$Exercice d\'electrostatique : Polarisabilité$

Posté par re : Exercice d'electrostatique : Polarisabilité 25-10-16 à 00:39

Merci, je pense avoir compris la question 1).

Maintenant pour la question 2 j'ai fais une erreur mais je ne sais pas où. Puisque a est négligeable devant R, je déduis que si M est dans la boule de centre O, alors elle l'est aussi dans la boule de centre O1 et O2.

Sachant que le champs pour un point intérieur M est :
E(M)= p*r/3*0, en appliquant le principe de superposition :

E(M) = E[O1](M) + E[O2](M)
Avec E[O1](M) = [-p*O1M/30 ]*u(O1M) où u(O1M) est le vecteur unitaire dirigé selon le vecteur O1M
Et donc puisque O1M = O1O + OM = (a/2 +R + e/2).

De même pour E[O2](M) avec la charge p positive.

Mais je ne tombe pas sur le bon résultat en sommant les 2.

De plus est-ce que je pourrai envoyer une image manuscrite de ce que j'ai fais ? Car je ne pense pas que ce soit très clair avec tout les vecteurs que je devrais écrire..

Posté par re : Exercice d'electrostatique : Polarisabilité 25-10-16 à 21:46

Bonsoir
Je crois que tu sais déterminer le champ créé par une boule uniformément chargée en volume. Si tu appliques le résultat, combiné au principe de superposition, pour un point M quelconque à l'intérieur de la boule de centre O et de rayon R, tu obtiens :

$\overrightarrow{E}=\frac{\rho}{3\varepsilon_{0}}\left(\overrightarrow{O_{1}M}-\overrightarrow{O_{2}M}\right)=\frac{\rho}{3\varepsilon_{0}}\cdot\overrightarrow{O_{1}O_{2}}=-\frac{\sigma_{0}}{3\varepsilon_{0}}\cdot\overrightarrow{u_{x}}$

où $\overrightarrow{u_{x}}$ est un vecteur unitaire dirigeant l'axe (Ox). Le champ électrique est donc uniforme à l'intérieur de la boule.

A l'extérieur de la boule, il faut repérer M par ses coordonnées polaires ( $r,\theta$ ) avec r > R. Deux coordonnées suffisent car la source de champ est invariante par rotation autour de l'axe (Ox). Le théorème de Gauss permet de montrer que le champ créé par une boule à symétrie sphérique de distribution de charge est celui que crée une charge ponctuelle placée au centre de la boule et égale à la charge totale de la boule. Si on pose : $Q=\frac{4}{3}\cdot\pi\cdot\rho\cdot R^{3}$ , le principe de superposition permet d'affirmer que le champ et le potentiel créés en M sont ceux créés par une charge Q placée en O₁ et une charge -Q placé en 0₂. Il s'agit donc du champ et du potentiel créés par un dipôle électrostatique de vecteur moment dipôlaire :

$\overrightarrow{p}=Q\cdot\overrightarrow{O_{2}O_{1}}=\frac{4}{3}\cdot\pi\cdot R^{3}\cdot\sigma_{0}\cdot\overrightarrow{u_{x}}$
La suite est classique : on calcule le potentiel V en M :

$V=\frac{Q}{4\pi\varepsilon_{0}}\left(\frac{1}{O_{1}M}-\frac{1}{O_{2}M}\right)$

Les expressions de $\frac{1}{O_{1}M}$ et $\frac{1}{O_{2}M}$ se détermine par une méthode analogue à celle suivie dans mon message précédent pour calculer e : théorème d'Al Kashi puis développement limité. On obtient ensuite l'expression du vecteur champ par la relation :

$\overrightarrow{E}=-\overrightarrow{grad}\left(V\right)$ .

Cette dernière partie est extrêmement classique : tu en trouveras plusieurs versions sur le net...