Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Exercice d'Electrostatique

Posté par
bill159 01-11-09 à 17:03

Après m'être acharné sur le cours, je passe aux exercices:

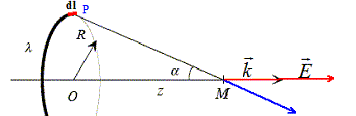
Soit une spire de rayon  R et un point M qui appartient à l'axe de cette spire.

Après avoir soigneusement démontré que dE = \frac{1}{{4\pi {\varepsilon _0}}} \times \frac{{\lambda dl}}{{{r^3}}}{u_r}

je m'attaque au calcul pour pouvoir déterminer l'intégrale de dE (donc la somme de toutes les charges élémentaires dq appartenant à un petit élément de l qu'on notera dl, voir figure.)

donc voila mes calculs:

\large \cos \alpha = \frac{z}{r}

\large r = \sqrt {{R^2} + {z^2}}
et enfin l'élément infintésimal dl:

\large dl = Rd\theta

Revenons à cette expression:

\large dE = \frac{1}{{4\pi {\varepsilon _0}}} \times \frac{{\lambda dl}}{{{r^3}}}{u_r}

on intègre et on a \large \int {dE = \frac{1}{{4\pi {\varepsilon _0}}} \times \frac{{\lambda dl}}{{{r^3}}}{u_r}}
je remplace dl par son expression et r^3 mais c'est là ou je bloque.  j'ai essayé de dire que {r^3} = {r^2} \times r

je remplace r par z/cos er r² par R²+z²

mais je bloque...

Merci d'avance

Exercice d\'Electrostatique

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:15

\large \int {dE = \int {\frac{1}{{4\pi {\varepsilon _0}}} \times \frac{{\lambda dl}}{{{r^3}}}{u_r}} \cdot k = \int {\frac{1}{{4\pi {\varepsilon _0}}} \times \frac{{\lambda dl}}{{{r^2}}}} } \times \frac{{\cos \alpha }}{z}{u_r} \cdot k

ensuite je bloque...

merci de m'aider

Posté par
donaldosre : Exercice d'Electrostatique 01-11-09 à 17:27

Ton expression de {\rm d}\vec{E} n'a pas l'air homogène à un champ électrique...

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:31

euh c'est à dire?

je vais revérifier les calculs...

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:34

ah oui

je réctifie:

\large dE = \frac{{\lambda dl}}{{4\pi {\varepsilon _0}{r^2}}}{u_r}

est-ce juste?

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:36

j'avais compris mon erreur, j'avais calculer le champ électrique créé par deux charges

c'est pour cela que j'avais r^3 au départ...

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:37

je prendrais alors un élément dE et je l'intégre entre les bornes 0 et 2

est-ce juste?

Posté par
donaldosre : Exercice d'Electrostatique 01-11-09 à 17:39

C'est juste maintenant.

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:41

mais après je bloque encore

comment faire

j'ai essayé changement de variable etc....

Merci d'avance

Posté par
donaldosre : Exercice d'Electrostatique 01-11-09 à 17:47

Pourquoi un changement de variable?

Après projection sur l'axe horizontal, l'intégrande ne dépend plus de \theta...

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 17:50

j'obtiens

\large E= \int\limits_0^{2\pi } {\frac{{\lambda dl}}{{4\pi {\varepsilon _0}{r^2}}} = } \int\limits_0^{2\pi } {\frac{{\lambda Rd\theta }}{{4\pi {\varepsilon _0}}} \times \frac{{{{\cos }^2}\alpha }}{{{z^2}}}}

je ne vois pas comment poursuivre

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:10

voila ce que j'ai essayé:

E = \int\limits_0^{2\pi } {\frac{{\lambda dl}}{{4\pi {\varepsilon _0}{r^2}}} = } \int\limits_0^{2\pi } {\frac{{\lambda Rd\theta }}{{4\pi {\varepsilon _0}{r^2}}}}

or \cos \alpha = \frac{z}{r} \Rightarrow r= \frac{z}{{\cos \alpha }}

je le remplace dans l'expression:

\large \int\limits_0^{2\pi}{\frac{{\lambda Rd\theta}}{{4\pi {\varepsilon _0}{r^2}}}}= \int\limits_0^{2\pi}{\frac{{\lambda Rd\theta}}{{4\pi {\varepsilon _0}{{\left( {\frac{z}{{\cos \alpha}}} \right)}^2}}}}= \int\limits_0^{2\pi}{\frac{{\lambda Rd\theta}}{{4\pi{\varepsilon _0}{z^2}}}}\times {\cos ^2}\alpha

mais j'ai aussi: z= \frac{R}{{\sin \alpha }}

donc je le remplace dans l'expression et je pourrai par la suite simplifier les R.

large \int\limits_0^{2\pi}{\frac{{\lambda Rd\theta}}{{4\pi {\varepsilon _0}{{\left( {\frac{R}{{\sin \alpha}}}\right)}^2}}}} \times{\cos ^2}\alpha= \int\limits_0^{2\pi}{\frac{{\lambda Rd\theta}}{{4\pi{\varepsilon _0}{R^2}}}}  \times{\cos ^2}\alpha {\sin ^2}\alpha= \int\limits_0^{2\pi}{\frac{{\lambda d\theta}}{{4\pi{\varepsilon _0}R}}}\times {\cos ^2}\alpha {\sin ^2}\alpha

Mais ensuite?

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:16

Pour info, c'est extrait du concours ITPE de l'année 2006  

Posté par
donaldosre : Exercice d'Electrostatique 01-11-09 à 18:22

On arrête le massacre?

Premièrement, tu as oublié de projeter {_rm d}\vec{E} sur \vec{k} avant d'intégrer.

Deuxièmement, je te l'ai déjà dit, rien dans ton intégrale ne dépend de la variable d'intégration! Tu peux donc tout en sortir:

\Bigint \frac{\lambda R \cos \alpha}{4\pi \epsilon_0 r^2^} {\rm d}\theta=\frac{\lambda R \cos \alpha}{4\pi \epsilon_0 r^2^} \Bigint {\rm d}\theta

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:29

ah oui c'est vrai!

et l'intégrale de dO donnera?

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:32

2pi bien sûr et je simplifie...

sire que j'ai passé bcp de temps dessus, la bêtise humaine est illimité.
Tu me sauve Donaldos

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:33

mais par contre j'ai pas compris ta projection dans le post de 18:22

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:38

j'aurais au final:

\large \int\limits_0^{2\pi } {\frac{{\lambda Rd\theta }}{{4\pi {\varepsilon _0}{r^2}}}}  = \frac{{\lambda R}}{{4\pi {\varepsilon _0}{r^2}}}\int\limits_0^{2\pi } {d\theta }

donc pas de cosinus ni rien

maintenant une autre question, pourquoi le potentiel est la primitive de E?

Merci d'avance

Posté par
bill159re : Exercice d'Electrostatique 01-11-09 à 18:51

oups j'ai oublier de rajouter cos

sinon après je remplace cos par z/r?


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !