Inscription / Connexion Nouveau Sujet
Exercice champ magnétique
Bonjour svp aide moi a résoudre ce problème. Voici l'énoncé
1) deux fils de longueur, rectilignes parallèles et distants de 1m, sont traverses par des courants de même sens. L'intensité commune est égale a 100A. Dans le plan des fils calculer
a) le champ magnétique résultant a égale distance de deux fils.
b) le champ magnétique a 2,5cm de l'une des fils, dans le plan forme par lesdeux fils. ( on précisera l'orientation de b sur un schéma).
***Forum et titre changés***
Pour résoudre cet exercice il faut :
a) Connaître les caractéristiques du champ magnétique créé en un point par un conducteur rectiligne parcouru par un courant, c'est-à-dire connaître la direction, le sens et le module de ce champ.
b) Savoir calculer les caractéristiques du vecteur champ résultant de la superposition des deux champs et
créés par les deux conducteurs.
Tout cela se trouve dans le cours ou à défaut sur internet.
Il serait donc intéressant que tu exposes ce que tu sais sur la question de manière à compléter ou à corriger d'éventuelles erreurs.
Bonjour merci davans de m'aider a résoudre cette exercice de magnetice. Voici l'énoncé :
Deux fils de longueur infinie, parallèles et distants de 1 m, sont traversés par des courants de même sens. L'intensité commune est égale a 100A. Dans le plans des fils. Calculer
a) le champ magnétique résultant égale distance des deux fils.
b) le champ magnétique a 2,5 cm de l'un des fils, dans le plan formé par les deux fils. ( on précisera l'orientation de B sur un schéma).
Voici les réponse
a) B=0 b) B=53,33Mt (B1=80Mt et B2=26,6Mt
*** message déplacé ***
Comme je le disais précédemment :
Il serait donc intéressant que tu exposes ce que tu sais sur la question de manière à compléter ou à corriger d'éventuelles erreurs.
Merci pour l'information j'essai de résoudre le problème mais je n'arrive pas. Est ce que tu peux me le résoudre svp. Merci pour ta compréhension.
j'essai de résoudre le problème mais je n'arrive pas
Si tu "n'arrive pas" c'est que tu as essayé. Alors fais nous part de tes essais.
Est ce que tu peux me le résoudre svp
Non : C'est à toi de résoudre et non à moi.
Voici les réponse
a) B=0 b) B=53,33Mt (B1=80Mt et B2=26,6Mt
Je ne sais pas ce que sont les "Mt". Ce symbole ne figure pas dans la liste des symboles du système international d'unités.
Pour t'aider un peu :
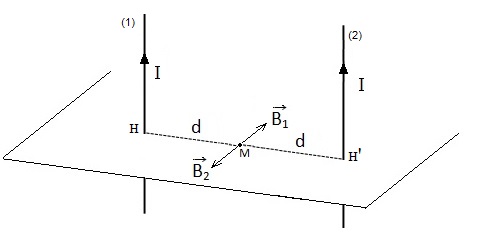
Tu trouveras ci-dessous un schéma destiné à illustrer la question 1
Le fil(1) engendre en M le champ magnétique
Le fil(2) engendre en M le champ magnétique
d est la distance entre un des fils et le point M
Tes énoncés sont bourrés d'erreurs.
Tu ne maîtrises absolument pas les symboles normalisés pour les préfixes dans les unités :
on a obligatoirement :
k (pour kilo qui multiplie par 10^3)
m (pour milli qui multiplie par 10^-3)
M (pour méga qui multiplie par 10^6)
(pour micro qui multiplie par 10^-6)
...
De plus, le symbole du Tesla est T et pas t.
Attention, il s'agit là d'erreurs majeures.
----------
De plus, par exemple pour l'exercice b, les réponses (même avec les préfixes des unités corrigés) ne collent pas avec les données de l'énoncé.
Si on a vraiment les distances de l'énoncé (soit 1 m et 2,5 cm), le rapport entre B1 et B2 ne peut pas être celui annoncé dans les "réponses".
-------------
Pour que l'énoncé puissent coller avec les réponses annoncées corrigées ( car des Méga Tesla sont un grosse sottise), il faut que l'énoncé soit celui-ci :
Deux fils de longueur infinie, parallèles et distants de 10 cm, sont traversés par des courants de même sens.
L'intensité commune est égale a 100 A. Dans le plans des fils. Calculer :
a) le champ magnétique résultant égale distance des deux fils.
b) le champ magnétique à 2,5 cm de l'un des fils, dans le plan formé par les deux fils. ( on précisera l'orientation de B sur un schéma).
-----------
Petit rappel théorique vers le milieu du lien suivant : ![]()
b)
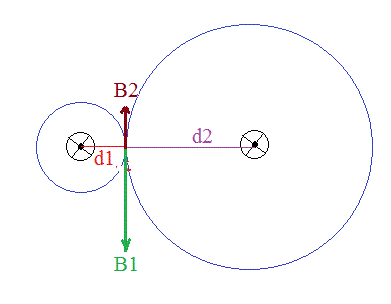
avec
et
avec µo = 4.Pi.10^-7 (SI) , I = 100 A, d1 = 0,025 m et d2 = 0,1 - 0,025 = 0,075 m ...
On arrive, sauf erreurs à : |B1| = 80 mT et |B2| = 26,7 mT
Doit donc à |B| = 80 - 26,7 = 57,3 mT
-----
Sauf distraction ... et en ayant modifié l'énoncé comme indiqué.

La question "a" et sa réponse associée m'embête.
Quid si le point M de odbugt1 n'est pas dans le plan des 2 fils mais ailleurs dans le plan médiateur des 2 fils ?
L'énoncé ne l'exclut pas ..., et la réponse n'est pas la même .... me semble-t-il

Bonjour, JP
Quid si le point M de odbugt1 n'est pas dans le plan des 2 fils mais ailleurs dans le plan médiateur des 2 fils ?
L'énoncé fourni par obamaroi est évidemment mal foutu, mais j'ai cru comprendre qu'il précisait que mon point M était bien dans le plan des 2 fils.
1) deux fils de longueur, rectilignes parallèles et distants de 1m, sont traverses par des courants de même sens. L'intensité commune est égale a 100A. Dans le plan des fils calculer
a) le champ magnétique résultant a égale distance de deux fils.
Bonjour. Oui vous avez raison et merci pou les correction c'est correcte. Sauf d=1m et non 10cm dans le livre. Bien que vous avez trouvez les bonnes reponses. Est ce que c'est une erreur. Et pour trouver B=0 comment vous procéder svp. Vous être génial. Et très compréhensive encore merci.
L'autre distance c'est d=25cm et non d=2,5cm merci je comprend l'exercice mais envois moi les démarche pour trouver B=0 svp.
La distance entre les fils n'impacte pas la valeur de la norme B1 du champ créé par celui des fils qui se trouve à d1 = 2,5 cm du point M étudié.
Je trouve B1 = 8.10-4T = 0,8mT (et non 80 mT)
Le point M se trouve dans le plan des fils à 2,5 cm de l'un d'entre eux, mais rien dans l'énoncé ne dit qu'il se trouve entre les deux fils. Il serait donc intéressant d'évoquer le cas ou d2 = d1 + D ( D : distance entre les deux fils)
Au fait : 8.10-5T = 0,08mT = 80 T
T
C'est probablement les "affreux" 80Mt proposés par obamaroi dans son énoncé !
Oui c'est bien la réponse et pour trouver la réponse a) comment vous procéder pour trouver B=0. Envois moi le démarche svp.
Re - bonjour,
Je ne fais que rarement le travail demandé aux élèves, et je ne le fais jamais quand ils ne proposent rien.
En revanche, je propose toujours une aide qui sera d'autant mieux ciblée que l'élève me montre à quelles difficultés il est confronté.
Sauf d'avoir relu ton énoncé et corrigé une donnée erronée tu n'as rien proposé.
Je vais donc juste t'inviter à relire mon message du 27/06 à 23h37 et revoir le schéma contenu dans mon message du 29/06 à 9h49
Les clés de la question 1 sont dans ces messages.
Oui, c'est exact.
En effet B1 et B2 ne dépendent que de l'intensité I et des distances d1 et d2.
Puisque I est le même pour les deux fils et que d1 = d2 on en déduit que B1 = B2
Les deux courants sont de même sens ce qui implique que les deux vecteurs champs sont opposés (même direction, sens contraire, même module) on en déduit que :
B = B1 - B2 = 0
D'accord merci pour votre aide et je félicité le forum. Avec vous je vais faire de mon mieux pour acquérir plus de connaissance.
J-P je comprend mieux tes schémas. Pouvez vous me résoudre l'exercice sur la rail de Laplace avec la solution et le schémas en borne et du forme svp. C'est dans le forum supérieur. Je compte sur vous. Merci d'avance


 ) :
) :

