Inscription / Connexion Nouveau Sujet
exercice bateaux
Bonsoir,
J'ai un devoir maison à faire (non noté, c'est juste pour le plaisir 
) et je suis bloquée dès le début.
Voici l'énoncé : (je joins à ce message les schémas nécessaires)
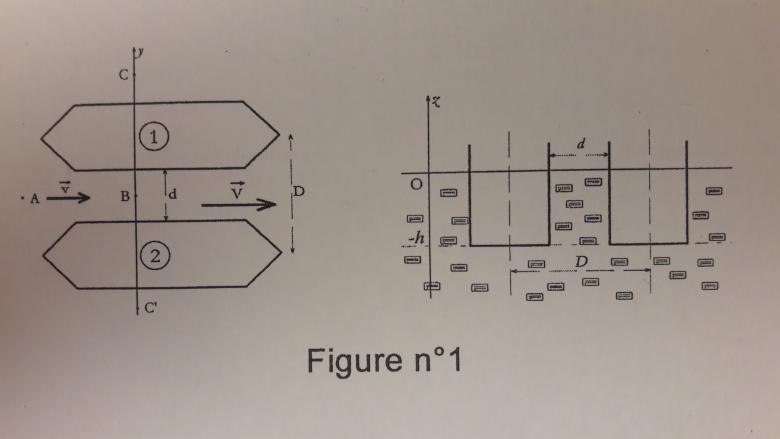
On considère deux navires identiques, assimilés à des parallélépipèdes de longueur L, terminés à l'avant et à l'arrière par deux dièdres.
On désigne par d la distance séparant leurs bords proches et par D la distance entre leurs plans de symétrie longitudinaux.
On dit qu'ils naviguent de conserve.
On se placera dans un repère lié aux bateaux, dans ce repère, les navires sont immobiles et c'est la mer qui est animée d'une vitesse constante notée .
Cependant, dans l'intervalle séparant les coques des navires, et jusqu'à la profondeur H, la vitesse de la mer est différente et on la note .
L'eau est considérée comme un liquide parfait.
On admettra que les écoulements sont laminaires et que le régime est permanent.
1. On considère un tube de courant délimité par deux plans horizontaux distants de , deux surfaces verticales passant par les lignes de courant arrivant sur la proue de chaque bateau. Calculer V en fonction de v, d et D.
Je posterai les questions suivantes si elles me posent problème aussi, mais pour l'instant je commence par le commencement.
Tout d'abord, j'avoue que j'ai du mal à voir dans quel chapitre du cours on se situe. Je ne sais pas s'il s'agit de mécanique "classique" ou plutôt de mécanique des fluides mais je pense quand même vu les hypothèses données qu'il s'agit surtout de mécanique des fluides. Ensuite, je ne vois pas dans quelle partie du cours on est précisemment. Est-ce qu'on est dans le chapitre de dynamique des fluides parfaits ou de la viscosité des fluides newtoniens ou un mélange des deux ?
Au départ, j'ai pensé au théorème de Bernoulli, mais il me semble que toutes les hypothèses nécessaires n'ont pas été faites : on ne nous dit pas qu'on suppose le fluide incompressible donc j'imagine qu'on ne peut pas se servir de cette relation.....
Du coup, je ne sais pas du tout d'où partir.....
Je ne comprends pas non plus cette première question : je n'arrive pas à visualiser la situation. A quoi correspondent les surfaces verticales ????
Enfin, dans l'énoncé, à quoi correspond H ? Est-ce que c'est la même chose que -h représenté sur le schéma ?
Merci d'avance pour votre aide !
Bonjour
Il s'agit clairement d'un problème de mécanique des fluides.
Sauf situations extrêmes toujours précisées dans les énoncés de problème, on peut considérer un liquide comme incompressible. En revanche (hors sujet ici mais cela te sera peut-être parfois utile) : un gaz n'est pas a priori considéré comme incompressible. Appliquer le théorème de Bernoulli à un gaz est donc une approximation qu'il n'est possible de faire que si l'énoncé le propose.
Pour la première question : raisonner sur la conservation du débit dans le repère galiléen lié aux bateaux me semble possible puisque le régime d'écoulement est permanent. Entre les deux bateaux, l'eau s'écoule entre deux parois verticales comme le montre le schéma "vue de face".
Merci pour tes indications. J'ai pu avancer un peu. En appliquant la conservation du débit volumique j'ai trouvé : V=vd/D
Est-ce que c'est juste ?
Questions suivantes :
2. Déterminer l'expression de l'écart de pression entre le point A loin des navires et le point B.
J'ai appliqué le théorème de Bernouilli entre A et B et j'obtiens :
Est-ce que c'est ça ?
3. On admet que la pression en tout point extérieur à la région comprise entre les navires est la même qu'en A.
Déterminer alors la force , perpendiculaire aux navires, qui s'exerce sur chaque bateau.
Je ne comprends pas ce que représente cette force et où elle se trouve sur le schéma vu qu'il y a deux schémas représentant les bateaux de deux manières "perpendiculaire" dans l'espace (même si ça ne se dit pas). J'imagine que c'est la force parallèle à d sur le 2e schéma mais je n'en suis pas sûre et je ne vois pas non plus d'où partir pour la calculer.....
On donne 
=1000kg/m3, L=50m, h=3m, v=5m/s, d=20m et D=25m.
D'accord avec ce que tu as fait .
La pression de l'eau entre les deux navires est donc inférieure à la pression de l'eau ailleurs ; la différence étant :
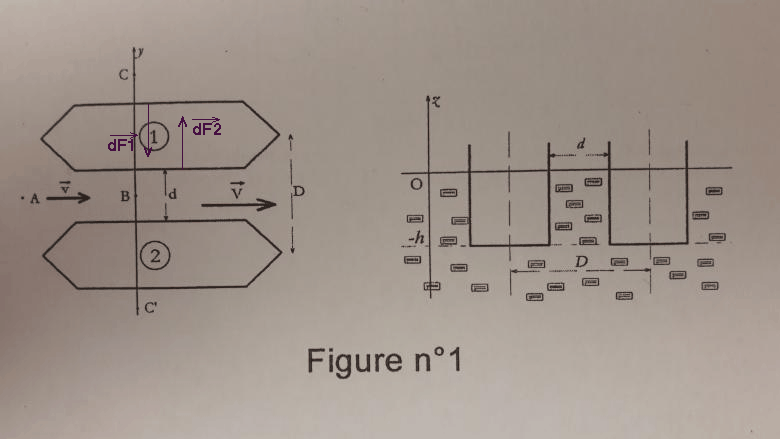
Considère maintenant une bande verticale d'une coque de navire de longueur L, de hauteur dz, située à la profondeur z, avec z compris entre zéro et h.
Si cette bande est située sur la parois extérieure de la coque, la pression en tout point de cette bande est la pressions statique P(z)=Patm+eau.g.z. I'eau exerce sur cette bande une force dF1 perpendiculaire à la coque exercée vers l'intérieur du navire, force qui tend à rapprocher les deux navires. Considère maintenant une bande identique, à la même profondeur mais située sur l'autre paroi de la coque. La pression de l'eau au niveau de cette bande est P(z)-
P. L'eau exerce donc sur cette bande une force dF2 perpendiculaire à la coque.
Inutile de déterminer chacune des deux forces : seule leur différence suffit. Je telaisse réfléchir ; tu devrais aboutir à la conclusion que l'eau tend à rapprocher les deux navires...
Je crois que je me suis trompée à la 1ere question : c'est
Ensuite, on a F= F1- F2= P
Or, D>d d'où v<V d'où PA>PB
Donc P>0
Alors F>0
Ainsi F1> F2
Donc l'eau tend à rapprocher les bateaux.
Est-ce que c'est ça s'il te plaît ?
OK pour tes inégalités mais attention : une force n'est pas égale à une pression !
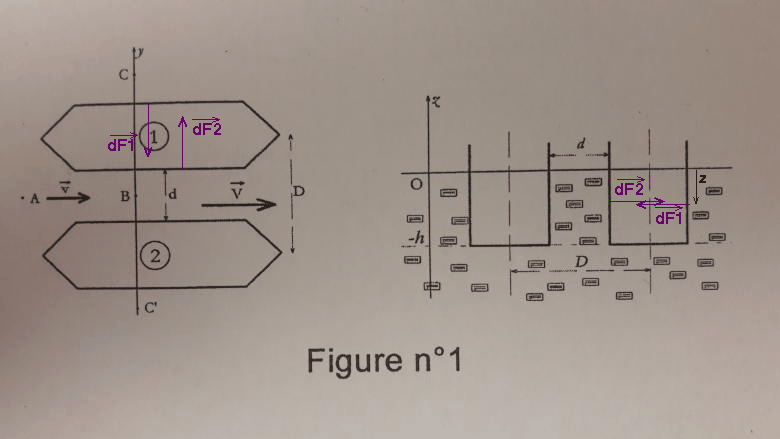
La résultante des deux forces : est un vecteur perpendiculaire à la coque qui tend à rapprocher ce navire de l'autre navire ; sa norme vaut :
P.L.dz
Si on intègre ce résultat de z=0 à z=h, on obtient une force exercée par l'eau sur un navire d'intensité :
F=P.L.h
Bien sûr, cette théorie simplifie beaucoup la réalité...
intensité de la force pressante : produit de la pression par l'aire de la surface pressée, pas quotient !
Euh oui pardon en plus c'est ce que je pensais dans ma tête au moment où je l'écrivais, j'ai même vérifié sur internet au cas où 
Du coup, c'est bon j'ai compris avec les mains pourquoi dF=P.L.dz mais je ne vois pas comment l'écrire sous la forme du calcul...
Je n'arrive pas à exprimer dF1 et dF2 parce-que je ne sais pas où il faut mettre les z.
Attention, ce que tu t'apprêtes à lire pique les yeux j'en ai bien conscience.
J'aurais eu tendance à écrire mais je sais que c'est faux:
Logiquement on devrait avoir un truc de la forme dF2=(pression x surface)dz mais je ne comprends pas comment on peut "retirer" le dz du g et comment faire pour que ce soit cohérent.....
Je l'avais écrit dans mon message de 12h22 : la pression statique à la profondeur z s'écrit :
; pas dz ! Donc :
Pour alléger les notations, je pose :
(
P>0)
Ces deux forces étant de même direction et de sens opposés, leur résultante a pour intensité :
Il suffit d'intégrer entre z= 0 et z=h, ce qui est très simple car ne dépend pas de z.
La direction et le sens de cette résultante sont ceux de la plus intense des deux forces précédentes : dF1 ; l'eau tend à rapprocher les deux bateaux.
Annuler
connectez vous