Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... Maths spéForum Supérieur de maths spe PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau maths spé
Partager :

Exercice basique

Posté par
numero10 18-09-10 à 14:16

Bonjour,

Je suis très mauvais en physique j'aurai besoin d'aide.

Citation :
On a une echelle de longueur l et de masse m qui est posé contre un mur sans frottement.On note A le point de contact de l'échelle avec le mur et B le contact de l'echelle avec le sol.

On notera R=(0,x,y,z) A appartient à (0z) et B à (0x)
et \theta=(\vec{BO},\vec{BA})
1)On me demande l'équation différentielle de la chute de l'échelle.

Moi bêtement j'ai utilisé le théorème de l'énergie cinétique:

0=d((1/2)m(l\fr{d\theta}{dt})^2 +mg(L\sin(\theta))

J'arrive alors à:

\fr{d^2\theta}{dt^2}+g\cos(\theta)/l=0

Peut on me dire ce qui ne va pas dans ce raisonnement et comment faut il procéder?

Merci d'avance

Posté par
Marc35re : Exercice basique 18-09-10 à 15:35

Bonjour,
Déjà, j'ai un problème avec l'énoncé...
A est le haut de l'échelle et B, le bas. Si A appartient à Oz et B appartient à Ox, pour moi, B et O sont confondus mais je me trompe peut-être.
D'autre part, c'est un mouvement de rotation donc il faut utiliser J'' = moment des forces

Posté par
numero10re : Exercice basique 18-09-10 à 17:14

Non B appartient à l'axe des x et l'échelle étant incliné O et B ne sont pas confondus .

Je vois pas trop ce que c'est cette formule sinon je vais regarder dans mon cours,et c'est quoi J? en tout cas merci

Posté par
numero10re : Exercice basique 18-09-10 à 19:39

Pouvez vous vérifier mon raisonnement svp?J'ai compris J on le note pas comme ça dans mon cours.

Donc comme on a un mouvement de rotation et ici,pour moi J_{AB}=(2/3)mR^2

Soit:

(2/3)ml^2\fr{d^2\theta}{dt^2}=gml(\vec{u_{AB}}\^\ \vec{u_z})

Soit:

\fr{d^2\theta}{dt^2}+\fr{3g}{2l}cos(\theta)=0

Posté par
numero10re : Exercice basique 18-09-10 à 19:56

Et désolé de multi poster mais c'est quoi une intégrale première du mouvement car c'est la question d'après?

Merci

Posté par
Marc35re : Exercice basique 18-09-10 à 21:21

J est le moment d'inertie de l'échelle. Il faut le calculer.
c'est l'équivalent de la 2ème loi de Newton mais pour les rotations.
Cela manque un peu de précision mais on peut l'assimiler à une barre homogène, je suppose...
3$J\,=\,\int_0^l\,x^2\,\rho\,dx\,=\,\frac{m\,l^2}{3}

Posté par
numero10re : Exercice basique 18-09-10 à 21:27

Ah oui effectivement donc je me suis planté j'avais pris J=(2/3)ml²

Posté par
numero10re : Exercice basique 18-09-10 à 21:35

Et au fait je ne sais pas calculer J (quoique je devrais je connais la formule) enfin j'ai un formulaire avec différentes valeurs que peut prendre J selon les cas.

Posté par
Marc35re : Exercice basique 19-09-10 à 11:51

"je ne sais pas calculer J" ==> en maths spé, c'est dommage...
Je reviens un peu plus tard.

Posté par
Marc35re : Exercice basique 19-09-10 à 13:09

La définition basique du moment d'inertie (qu'on appelle J ou I en général), c'est pour une masse ponctuelle à la distance d du centre :
J\,=\, m\,d^2
Quand on a plusieurs masses ponctuelles :
J\,=\,\sum_i\,m_i\,d_i^2
Quand on a un solide continu, il faut intégrer. Par exemple, une barre de longueur l et de masse m fixée à une extrémité. On considère la masse élémentaire dm = dx  située à la distance x :
(on considère que le problème est à une dimension)
2$J\,=\,\int_0^l\,\rho\,dx\,x^2
  étant la masse linéique
2$J\,=\,\rho\,\int_0^l\,x^2\,dx\,=\,\rho\,[\frac{x^3}{3}]_0^l
2$J\,=\,\rho\,\frac{l^3}{3}
3$J\,=\,\frac{m\,l^2}{3}

On peut considérer l'échelle comme une barre...
on peut calculer le moment d'inertie d'un disque, par exemple, ou d'une sphère de la même façon en essayant de se ramener à une dimension (c'est plus facile).
Mais, normalement, tu dois avoir vu ça en cours...

OK ?

Posté par
Marc35re : Exercice basique 19-09-10 à 13:11

J_{AB}=(2/3)mR^2
ça doit être pour un disque de rayon R...

Posté par
Marc35re : Exercice basique 19-09-10 à 13:12

J_{AB}=(2/3)mR^2   (l'aperçu, c'est utile ! )
ça doit être pour un disque de rayon R...

Posté par
numero10re : Exercice basique 19-09-10 à 13:54

Oui tout est ok c'est très bien détaillé merci et effectivement c'était pour un disque de rayon R.Dans ma section en MP j'ai un poly où il est écrit que c'est non exigible.Pourtant c'est vrai que ce n'est pas ce qu'il y a de plus dur.Du coup je n'ai pas vu ça en cours.
Pourrais tu me dire aussi ce qui ne va dans l'équation différentielle que j'ai établie à part la valeur de J ?

Posté par
Marc35re : Exercice basique 19-09-10 à 16:02

J '' = moment des forces

3$\frac{ml^2}{3}\,\frac{d^2\theta}{dt^2}\,=\,\frac{mglcos\theta}{2}

3$\frac{d^2\theta}{dt^2}\,=\,\frac{3}{2}\,\frac{g\,cos\theta}{l}

Posté par
numero10re : Exercice basique 19-09-10 à 16:14

En fait d'où provient le /2 ? Et le produit vectoriel donne un moins , quoique ça doit dépendre de comment on a orienter thêta.

Posté par
Marc35re : Exercice basique 19-09-10 à 17:06

Les moments des forces dus aux différents morceaux de l'échelle ne sont pas les mêmes parce qu'ils ne sont pas situés à la même distance du pivot.
Donc il faut découper l'échelle en morceaux de longueur dr à la distance r et de masse dr
3$\vec{dM}\,=\,\vec{BM}\,\wedge\,\vec{dF}
3$\vec{dM}\,=\,-\,r\,\rho\,g\,dr\,cos\theta\,\vec{y}
3$\vec{M}\,=\,-\,\rho\,g\,cos\theta\,\int_0^l\,r\,dr\,\vec{y}\,=\,-\,\rho\,g\,cos\theta\,[\frac{r^2}{2}]_0^l\,=\,-\,\rho\,g\,cos\theta\,\frac{l^2}{2}

4$\vec{M}\,=\,-\,\frac{m\,g\,l\,cos\theta}{2}

Effectivement, il y a un signe - .
Donc :

4$\frac{d^2\theta}{dt^2}\,=\,-\,\frac{3}{2}\,\frac{g\,cos\theta}{l}

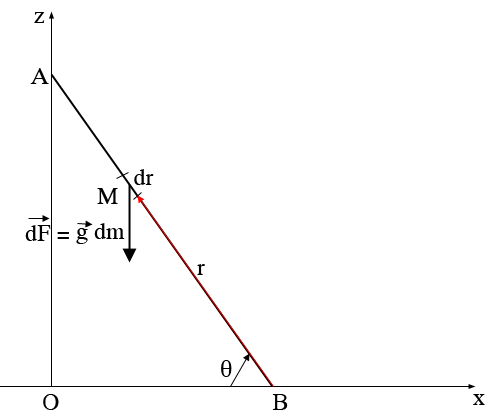
Exercice basique

Posté par
Marc35re : Exercice basique 19-09-10 à 17:08

L'axe y est effectivement perpendiculaire à la feuille (ou à l'écran) et orienté vers l'arrière afin que le trièdre soit direct.

Posté par
numero10re : Exercice basique 19-09-10 à 18:55

Ok,merci bien il manque parfois des vecteurs ce doit être le vecteur unitaire selon y.Je vais reprendre tous ça au calme.Sinon savez vous ce qu'est une intégrale première j'ai cherché sur internet il s'agirait d'écrire une égalité sur les énergies?

Posté par
Marc35re : Exercice basique 19-09-10 à 19:27

Oui, j'ai perdu le vecteur unitaire  \vec{y}   en cours de route  
Il suffit d'intégrer le  \frac{d^2\theta}{dt^2}, pour trouver   \frac{d\theta}{dt}

Posté par
numero10re : Exercice basique 19-09-10 à 19:57

Ah bon je devrais m'en sortir alors merci beaucoup pour toute cette aide.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !