Exercice AOP , exercice de Physique

 Niveau autrePartager :
			        
Exercice AOP 
Posté par 
Altaiir95  19-12-15 à 20:43
Bonsoir, 

J'aurai grandement besoin d'aide pour résoudre la 2eme question de cet exercice svp, 

On considère le circuit de la figure suivante :  
1) Calculer la tension u en fonction de us, ue et des résistances
2) Calculer le courant Is dans la charge Ru en fonction de Us, Ue et des résistances 
3) Quelle relation doivent vérifier les résistances pour annuler le coefficient de us dans l'expression de is ?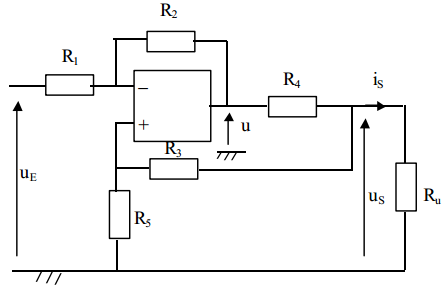 

Pour la 1ere question, je n'ai pas eu de mal en appliquant le théoreme de Millman, mais parcontre pour la 2eme question, je bloque complètement, j'ai essayer de trouver les expression des courant I et I' ( I est celui qui circule dans R4 et I' celui qui circule dans R3), pour I j'ai trouvé U/R4, pour I' j'ai trouvé : Us/R3 ( ce qui est faux je pense, mais je n'ai pas d'autres idée :/) 

Merci

***Edit gbm : image insérée sur le serveur et recadrée, merci de faire de même la prochaine fois !***
 Posté par 
sanantonio312re : Exercice AOP   20-12-15 à 09:07
Bonjour,

il faudrait le schéma pour t'aider...
 Posté par 
Altaiir95re : Exercice AOP   20-12-15 à 10:26
Bonjour, 

Désolé je n'avais pas bien inséré l'image, merci au modérateur qui a édité mon poste ^^ 
 Posté par 
sanantonio312re : Exercice AOP   20-12-15 à 10:48
Qu'as-tu trouvé à la première question?
 Posté par 
sanantonio312re : Exercice AOP   20-12-15 à 10:51
La question 2 me paraît etrange (trop simple): is=us/Ru
 Posté par 
J-Pre : Exercice AOP   20-12-15 à 11:59
Les questions sont un peu bizarres si on ne voit pas où l'auteur veut en venir.

Je pense que le but final de l'auteur est de faire un générateur de courant règlable ...

Donc avoir une réponse de circuit telle que is = k.ue avec k une constante (donc is indépendant de la valeur de Ru, et donc de us)

Pour y arriver, il faut arriver à écrire is = f(ue, R1, R2 , R3,R4,R5, Ru) 

Et ensuite s'arranger pour que le terme comprenant Ru s'annule de l'expression (en choisissant les valeurs adéquates pour les autres résistances)

Lorsque ce sera fait, je pense qu'on aura atteint le but, soit avoir une réponse du circuit telle que is = k.ue

 Posté par 
Altaiir95re : Exercice AOP   20-12-15 à 12:31
Bonjour et merci pour vos réponses  

Voici les résultat que l'on doit trouver selon le corrigé de l'exercice, pour la 1ere question j'y suis arriver sans trop de difficulté mais la 2eme .. :/ 

 Posté par 
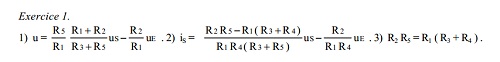
J-Pre : Exercice AOP   20-12-15 à 15:40
Je l'ai fait par une autre voie que celle préconisée. Tant pis.

us/[Ru(R3+R5)/(R3+R5+Ru)] = u/[R4 + Ru(R3+R5)/(R3+R5+Ru)]

us/(Ru(R3+R5)) = u/(R3R4+R4R5+Ru(R3+R4+R5))

et connaissant u = ... (question 1) -->

us/(Ru(R3+R5)) = (R5/R1 * (R1+R2)/(R3+R5).us - R2/R1 * ue)/(R3R4+R4R5+Ru(R3+R4+R5))

us * [(R3R4+R4R5+Ru(R3+R4+R5))/(Ru(R3+R5)) - R5/R1 * (R1+R2)/(R3+R5)] = -R2/R1 * Ue

us/Ru * [(R3R4+R4R5+Ru(R3+R4+R5))/(R3+R5) - Ru * R5/R1 * (R1+R2)/(R3+R5)] = -R2/R1 * Ue

is * [(R3R4+R4R5+Ru(R3+R4+R5))/(R3+R5) - Ru * R5/R1 * (R1+R2)/(R3+R5)] = -R2/R1 * Ue

Si on veut que us n'intervienne pas dans la relation, il suffit de neutraliser le terme contenant Ru.

Pour ce faire, il faut que (R3+R4+R5)/(R3+R5) - R5/R1 * (R1+R2)/(R3+R5) = 0

Soit donc que R1.(R3+R4+R5) - R5(R1+R2) = 0

--> R1.(R3+R4) - R5R2 = 0

R2R5 = R1.(R3+R4)  (Qui est la réponse à la question 3)

On a alors : is * (R3R4+R4R5)/(R3+R5) = -R2/R1 * Ue

is * R4 = -R2/R1 * Ue

is = -R2/(R1.R4) * Ue

(qui est la réponse 2 dans laquelle on a neutralisé le terme en us)

-----

Donc si on s'arrange pour avoir : R2R5 = R1.(R3+R4), alors le montage se comporte en générateur de courant règlable (par la valeur de R2) avec is = -R2/(R1.R4) * Ue

Sauf distraction.  
 Posté par 
prepa1997re : Exercice AOP   20-12-15 à 15:49
comment vous faites pour déterminer les condition intiales et a l'infinie des circuits ?
 Posté par 
Pirhore : Exercice AOP   20-12-15 à 17:51
Bonjour,

Je pense que tu avais une bonne idée en ajoutant les courants mais tes expressions 
Citation :
pour I j'ai trouvé U/R4, pour I' j'ai trouvé : Us/R3 
 sont fausses.

En remplaçant u par sa valeur, on trouve bien:

 Posté par 
J-Pre : Exercice AOP   20-12-15 à 18:28
Petite distraction de Pirho dans sa dernière ligne.

Remplacer "R1+R4" par "R1*R4"

 Posté par 
Pirhore : Exercice AOP   20-12-15 à 18:50
Salut J_P 

Of course!

Mauvaise recopie  
 Posté par 
J-Pre : Exercice AOP   20-12-15 à 19:42
Salut Pirho

  Posté par 
Altaiir95re : Exercice AOP   20-12-15 à 23:11
Merci à vous, je n'avais pas compris mon erreur, pour moi la tension US n'entrer pas dans la maille, comme quoi je suis loin de maîtriser ces lois correctement :/