Niveau licence

exercice acoustique (anglais)

Posté par
louis293 30-11-16 à 22:51

bonjour, je suis en sejour erasmus et je galère un peu avec un exercice d'acoustique dans mes etudes díngenieur, je ne comprend pas bien le sens de la question , l'ennonce est le suivant:
"On a 2D plane,we position an array of 2N+1 omnidirectionnel microphones, arranged symmetrically on the y axis and around the origin. The inter-microphone is d.

1 Express the signal captured by each microphone of the array for a generic complex plane wave of amplitude a, incident from direction . If all the microphone are combined (summed) together, show that the effect of the array to the plane wave is a real function of and find the direction for which the array to the plane wave is a real function of , and find the directions for which the maximum response and the amplification that imposes to the plane wave, photo avc schema

je ne comprend pas bien la question faut il partir dún signal du type a exp(-ikl) (onde plane) calculer la phase a chacun des points avec une analyse geometrique et faire la somme, je ne comprend pas vraiment ce quón entend par effet sur l'onde

je vous remercie d'avance si vous avez des pistes

Posté par re : exercice acoustique (anglais) 30-11-16 à 23:43

j'ai oublie de mettre la photo le schema

exercice acoustique (anglais)

Posté par re : exercice acoustique (anglais) 01-12-16 à 14:43

Bonjour
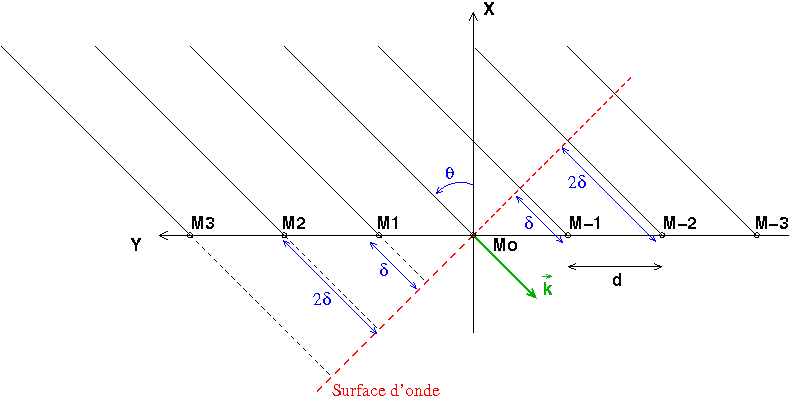
Je pense que tu sais ce qu'est une onde plane. Ici l'onde plane se propage suivant la direction et le sens du vecteur d'onde $\overrightarrow{k}$   de norme $k=\frac{2\pi}{\lambda}$ . J'ai représenté en pointillé rouge la trace dans le plan de figure de la surface d'onde. En tout point de cette surface d'onde, le signal acoustique est le même. En choisissant arbitrairement nulle la phase initiale du signal en tout point de cette surface, l'expression de ce signal est $s_{0}=a.\cos\left(\omega t\right)$ . Comme en électrocinétique des régimes sinusoïdaux, le complexe associé à ce signal est :

$\underline{s_{0}}=a.e^{j\omega t}$
Le micro Mo appartenant à cette surface d'onde, le signal qu'il reçoit est $\underline{s_{0}}$ . Le micro M1 est situé devant la surface d'onde, à la distance $\delta=d.\sin\left(\theta\right)$ . Le signal reçu en M1 est donc en avance de phase par rapport à celui reçu en Mo :

$\underline{s_{1}}=a.e^{j\left(\omega t+\Phi\right)}\quad avec\quad\Phi=k.\delta=\frac{2\pi.d.\sin\left(\theta\right)}{\lambda}$
Le schéma est explicite : on obtient de même :

$\underline{s_{2}}=a.e^{j\left(\omega t+2\Phi\right)}\quad;\quad\underline{s_{3}}=a.e^{j\left(\omega t+3\Phi\right)}\quad;\quad....\$
En revanche, le micro M-1 est situé derrière la surface d'onde.Le signal reçu en M-1 est donc en retard de phase par rapport à celui reçu en Mo :

$\underline{s_{-1}}=a.e^{j\left(\omega t-\Phi\right)}\quad;\quad\underline{s_{-2}}=a.e^{j\left(\omega t-2\Phi\right)}\quad;\quad\underline{s_{-3}}=a.e^{j\left(\omega t-3\Phi\right)}\quad;\quad....$
Le signal somme des différents signaux a pour complexe associé :

$\underline{s}=a.e^{j\omega t}.\left(e^{-jN\Phi}+e^{-j\left(N-1\right)\Phi}+...+e^{-j\Phi}+1+e^{j\Phi}+...+e^{j\left(N-1\right)\Phi}+e^{jN}\right)$

Deux méthodes possibles maintenant pour obtenir l'amplitude A de la somme.

Première méthode : remarquer que, quelquesoit le nombre n : $e^{jn\Phi}+e^{-jn\Phi}=2.\cos\left(n\Phi\right)$ . L'amplitude du signal somme est ainsi :

$A=a\left[1+2.\cos\left(\Phi\right)+2.\cos\left(2\Phi\right)+...+2.\cos\left(N\Phi\right)\right]$
On remarque que si : $\Phi=0$   modulo $2\pi$ , tous les cosinus sont égaux à 1 : l'amplitude est maximale et égale à :

$A_{max}=\left(2N+1\right).a$
Dans ce cas particulier, les signaux reçus par les (2N+1) micros sont en phase : les amplitudes s'additionnent.

Cette méthode permet d'obtenir les maximums d'amplitude mais ne permet pas une étude précise et simple (tout est relatif...) des variations de l'amplitude A en fonction de $\Phi$ . La seconde méthode, plus rigoureuse, consiste à partir de l'expression de $\underline{s}$   en multipliant tous les termes par : $1=e^{-jN\Phi}.e^{jN}$ . Cela donne :

$\underline{s}=a.e^{j\left(\omega t-N\Phi\right)}.\left(1+e^{j\Phi}+e^{2j\Phi}+...+e^{2jN\Phi}\right)$
La somme des termes entre parenthèses est facile à calculer si tu connais les propriétés des suites géométriques. Il suffit ensuite d'écrire que l'amplitude est : $A=\sqrt{\underline{s}\cdot\underline{s}*}$ où $\underline{s}*$ désigne le complexe conjugué de $\underline{s}$ ... Je te laisse réfléchir à tout cela et terminer les calculs. N'hésite pas à poser d'autres questions si tu le juges utile.
Remarque : l'énoncé appelle l'angle caractérisant la direction de propagation de l'onde alors que la figure la note . J'ai fait le premier choix...

exercice acoustique (anglais)

Posté par re : exercice acoustique (anglais) 01-12-16 à 16:00

Petite "coquille" dans une formule que tu as sans doute rectifiée par toi même : pour ne pas modifier l'expression de s, il faut multiplier tous les termes par :

$1=e^{-jN\Phi}.e^{jN\Phi}$

Posté par re : exercice acoustique (anglais) 01-12-16 à 16:07

Le même oubli : expression de s :

$\underline{s}=a.e^{j\omega t}.\left(e^{-jN\Phi}+e^{-j\left(N-1\right)\Phi}+...+e^{-j\Phi}+1+e^{j\Phi}+...+e^{j\left(N-1\right)\Phi}+e^{jN\Phi}\right)$

Posté par re : exercice acoustique (anglais) 02-12-16 à 14:31

Waouh, merci bcp pour la reponse cest tres clair maintenant,

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

exercice acoustique (anglais)

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique