Inscription / Connexion Nouveau Sujet
Exercice A.O étude d'un oscillateur - gbm
Bonjour à tous,
je suis en train de faire un extrait d'un problème, et j'aurais besoin de votre avis sur cette partie :
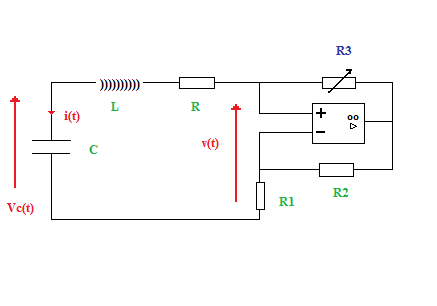
Dans ce circuit, l'amplificateur opérationnel est idéal et fonctionne en régime linéaire.
R3 est réglable.
[img2]
1. Etablir la relation entre i(t), v(t), R1, R2 et R3.
2. En déduire l'équation différentielle vérifiée par i(t).
On posera ,
et
.
3. Etudier qualitativement le fonctionnement du motage lorsque
* m' > m
* m > m
Que se passe-t-il si m = m' ? Cette condition est-elle réalisable ? Quel est le rôle de R3 ?
A.N : C = 22 nF, L = 20 mH. A quelle fréquence peut fonctionner cet oscillateur ?
-------------------------------------------------------------------------------------
Réponses :
1) A.O idéal => i+ = i- = 0 et fonctionne en régime linéaire.
Donc
v(t) = (R1 + R2 + R3).i(t)
Je sais ma question est bête mais c'est la sortie de l'A.O qui m'embête...
Merci pour l'aide que vous pourrez m'apporter.

sauf erreur,on peut écrire
R3i +R2i' =0
i'=-(R3/R2)i
Vt=0 + R1i'=-(R1R3/R2)i
L(di/dt) +Ri +q/C +R1i' =0
L(di/dt) +Ri +q/C -(R1R3/R2)i=0
L(d2i/dt2)+ (R-R1R3/R2)(di/dt) +i/C =0
à confirmer
je continue,
L/R=2m 0
0
R1R3/R2L=2m' 0
0
l'équation devient
Ld2i/dt2 + 2 0(m-m')di/dt +
0(m-m')di/dt + 2i=0
2i=0
si m-m'=0 l'équation se réduit à
d2i/dt2 + 2=0
2=0
dont la solution est du type
i=M sin( t+
t+ )
)
c'est donc un régime sinusoïdal non amorti
dans le cas où m>m' ou m<m' ,je coince ,car mes connaissances sur les équa dif sont lointaines A dire vrai ,je ne vois pas la différence entre les deux cas
le polynôme caractéristique s'écrit
X2 +2 0(m-m')X +
0(m-m')X + 2
2
le déterminant est
 =4
=4 2(m-m')2 -4
2(m-m')2 -4 02=4
02=4 02[(m-m')2-1]
02[(m-m')2-1]
je ne vois pas en quoi m>m' ou m<m' change quoi que ce soit
par contre le signe de (m-m')2-1 déterminera la nature des racines (complexes ou réelles)
mais je me suis peut-être trompé
salut gbm
As tu replanché sur cet exo?J' ai quelque doute sur mes réponses.Ce n'est pas un domaine que j'ai enseigné.
Salut Coriolan, je t'ai répondu sur un autre topic :
je vais regarder cela d'un peu plus près demain. J'avais fait une grave erreur en considérant que l'intensité était la même en tout point du circuit (y compris à la sortie de l'A.O !).
Je te dirai ça un peu plus tard 
Voici ce que j'ai :
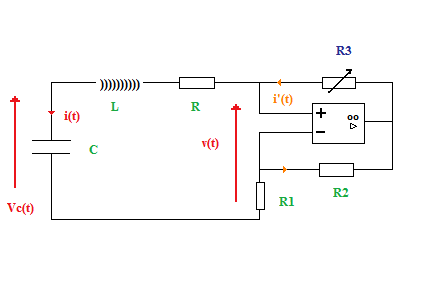
1. L'A.O est idéal : i+ = i- = 0 et fonctionne en régime linéaire donc  =0.
=0.
La loi des noeuds est traduite sur le schéma.
D'après la loi des mailles :
v(t) =  - R1 i'
- R1 i'
R3 i + R2 i' +  = 0
= 0
donc et
2. D'après la loi des mailles : et
donc
<=>
d'où en utilisant les données de l'énoncé :
et de même,
3. Si m' < m, le coefficient devant di/dt est positif. On a donc un régime amorti (avec des exponentielles décroissantes).
Si m' > m, le coefficient devant di/dt est négatif. On a donc pour i une solution avec des exponentielles croissantes, donc une amplification de i au cours du temps, qui va entraîner une saturation de l'A.O.
Pour m = m', l'équation différentielle devient :
d'où i est une fonction sinusoïdale du temps.
Pour avoir m' = m, il faut régler R3 pour avoir R = R1.R3/R2.
Voilà 
Bonjour GBM
merci d'avoir pris le temps de rédiger ta réponse.
j'ai vu que j'ai fait 2 fautes d'inattention.
ce qui m'intéressait surtout c'était la discussion concernant le signe de m -m'.
Quelles études suis -tu ,si ce n'est pas indiscret?
Quelles études suis -tu ,si ce n'est pas indiscret ?
2ème année de prépa (filière PT), pourquoi ?

simple curiosité.Je suis épaté (et admiratif ) qu'un étudiant en classe prépa consacre autant de temps à ce forum.
Oh, tu sais, j'aime bien aider les personnes en difficulté en physique et maths.
De plus, je me dis qu'en faisant des exos de base, cela m'entraîne moi aussi quelque part.
En effet, très souvent, les concours sont truffés de questions simples qui ne sont pas traitées par la plupart des étudiants (je parle des dosages par exemple). En en faisant régulièrement sur le forum, cela me permet d'être rapide pour ce genre de questions.
Tu remarqueras que j'y reste peu en semaine, mais un peu plus de temps le week-end 
Bonjours à vous,
J'ai traité l'exercice que vous proposez en TD mais je n'ai pas eu la correction ou du moins pas encore. J'ai trouvé l'équation différentielle et avec l'aide de ce sujet j'ai tiré les mêmes conclusions pour la dernière question.
Mon problème est plutôt l'application numérique que vous avez laisser de coté, je ne vois pas comment on peut déduire les fréquences limites de fonctionnement de l'oscillateur. Je me doute qu'il y a un lien entre la saturation de l'A.O et la fréquence mais je ne le trouve pas.
Un élève de Maths Sup désireux d'apprendre.
Ps: Sauriez vous de quel concours est tiré cet exercice?

 LCo)
LCo)
 )
) 7587,4 Hz
7587,4 Hz


