Inscription / Connexion Nouveau Sujet
exercice
Bonjour
j'ai un exercice d'électrocinétique où je bloque sur une question : déterminer les 3 équations littérales des courants dans chaque branches (vous devrez trouver : | I1| = 0.32A, | I2 | = 0.41A et | I3 | = 0.73A)
Le schéma est en pièce jointe
J'ai trouvé pour la loi des n?uds : I1 +I2 +I3 =0
Mais je suis bloquée pour la loi des mailles....
Pourriez-vous m'aider ?
Merci d'avance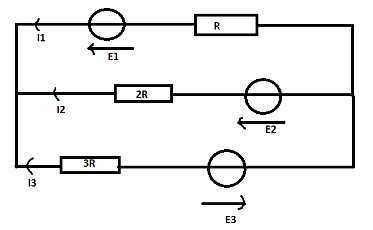
***Image recadrée***
Bonsoir,
Ton montage compte trois mailles: celle parcourant,
-les branches 1 et 2
-les branches 2 et 3
-les branches 1 et 3
Tu peux appliquer la loi des mailles à chacune de ces mailles.
(en fait il suffira d'en faire que deux ; la troisième se déduisant des deux précédentes)
d'accord mais je ne sais pas comment appliquer concrètement la loi des mailles avec deux générateurs
Additionne simplement les différences de potentiel.
Exemple avec la maille parcourant les branches 1 et 2:
On va appliquer la loi des mailles (je décide de tourner dans le sens des aiguilles d'une montre)
aux bornes de R1 : u1 = -RI1
aux bornes de E1 : u2 = E1
aux bornes de R2: u3 = 2RI2
aux bornes de E2: u4 = -E2
La loi des mailles donne donc u1+u2+u3+u4=0
Donc on a :
E1 - RI1 + 2RI2 -E2
ET
E1 - RI1 + 3RI3 + E3
mais je ne trouve absolument pas les résultats attendus :/
Attention ce que tu as écrit ne sont pas des équations (tu as oublié "=0")
Finalement le système à trois inconnus I1, I2, I3 à résoudre est le suivant :
Montre moi ta résolution
On a donc
2R * (1) : 2RI1 + 2R I2 +2RI3 =0 (1')
(2) - (1') : E1 - E2 -3RI1 - 2RI3 = 0 (2')
3*(3) + (2') : 3E1 - 3RI3 +6RI3 +3E3 - E1 +E2 +3RI1 + 2RI3 =0
==> -2E1 + E2 + 8RI3 + 3E3 = 0
Donc I3 = (2E1 - E2 -3E3)/8
Oui, mais attention pour la dernière manipulation 3(3)-(2'):
3E1-3RI1+9RI3 + 3E3 - E1 + E2 + 3RI1+2RI3 = 0
==>+2E1 + E2 +11RI3+3E3 = 0
==> I3 = -(2E1+E2+3E3)/11
Une méthode qui marche bien pour se dépatouiller avec un système de la sorte et d'injecter l'équation (1) dans les deux autres. Ainsi on se ramène à un système de deux équations à deux inconnues qui peut se résoudre par combinaison linéaire.


