Inscription / Connexion Nouveau Sujet
Etude du régime statique appliqué à une particule de mvt tri
Bonjour les amis , j'espère que vous allez bien .. Je me suis bloqué sur cette partie d'un exercice (Piège de paul pour les ions ) . une formule donnée : Ep(x,y,z)=f(ax^2+ay^2+bz^2) avec Ep l'energie potentielle . et f dépend de la charge de la particule et de la tension U et a et b deux constantes
Le mouvement de cette particule se fait tout en subissant une seule force qui dérive de l'énergie potentielle ;
Ils me demandent d'exprimer F (vecteur ) en fonction de a b ,f0 , x ,y,z et des vecteurs associés ( avec f0=f régime statique )
Je me bloque totalement , je sais pas d'où commencer
Bonjour
Lorsqu'une force dérive d'une énergie potentielle (force conservative), le vecteur force est donnée par l'expression :
Tu connais sûrement l'expression du gradient en coordonnées cartésiennes...
Ouais , mais ce qui me cause de problème c bien la fonction . est ce que c suffisant de l'exprimer sous forme de 2ax *df0(ax^2+...)/dx +...+... ?
Oui c ce que j'avais fais
bon après ils me donnent 2a+b=0 et me demandent de déduire quant à la possibilité de pièger une une particule chargée
Tu peux te demander si, en présence de cette seule force électrique, une position d'équilibre stable existe.
Dans ces conditions, tu peux écrire l'énergie potentielle sous la forme :
Tu peux alors démontrer que la force électrique est nulle en (0,0,0) puisque les trois dérivées par rapport à x, y, z sont nulles en ce point. En revanche, quel que soit le signe de a, il est impossible que les trois dérivées secondes soient toutes trois positives en ce point. L'équilibre est donc instable.
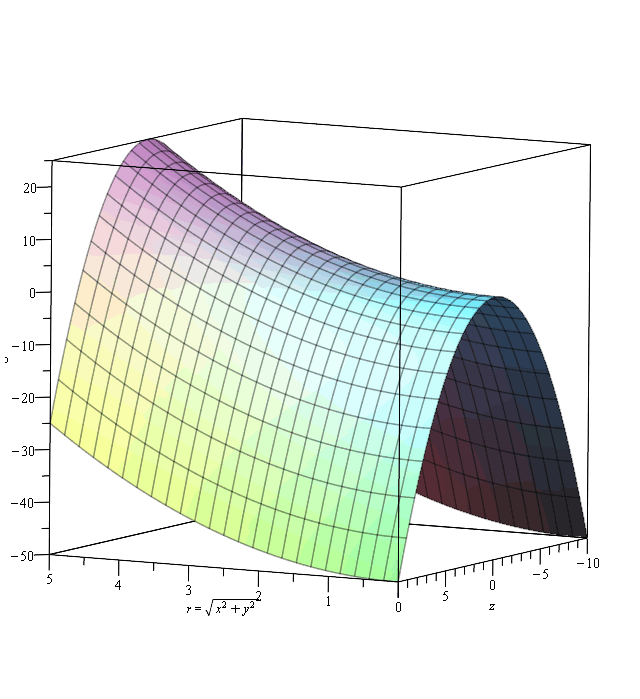
Pour bien comprendre comment évolue l'énergie potentielle en fonction des coordonnées d'espace, on peut remarquer que : où r désigne la distance à l'axe (Oz). L'énergie potentielle est donc invariante par rotation autour de l'axe (Oz).