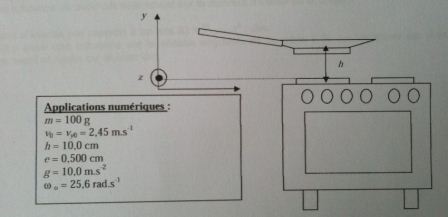
désolé pour le double poste mais j'ai oublié de dire que la crêpe partait de la hauteur h de la plaque de cuisson et a t=0 la crêpe décolle de la poêle. Le cuisinier repose ensuite la poêle sur la plaque. Au cours de son mouvement, la crêpe est considérée comme étant en chute libre.

salut
juste une question avant de t'aider, on considère la crèpe comme un point matériel ? à quoi se rapport le oméga 0 dans les données ?

oui elle est considérée comme ponctuelle et oméga 0 c'est pour la 2eme partie de l'exo quand la crêpe est considérée comme un disque

en fait l'énoncé exacte c'est  : Le cuisinier lance la crêpe d'une poêle d'épaisseur e avec une vitesse v0 verticale dirigée vers le haut. La crêpe est initialement à une hauteur h de la plaque de cuisson. L'instant t=0 correspond à l'instant où la crêpe décolle de la poêle. Le cuisinier repose ensuite la poêle sur la plaque chauffante. Au cours de son mouvement, la crêpe est considérée comme étant en chute libre.

Question : déterminer l'équation horaire y(t) du mouvement de la crêpe en fonction de vy0, g et du temps t dans le plan vertical, y désignant la verticale ascendante.

bon alors imaginons qu'on reste en mécanique du point.
tu as fait des exos comme ça en terminale je pense. La crêpe est en chute libre donc :
m.a = -m.g  (PFD projeté sur l'axe y)

a = - g

ensuite il te suffit d'intégrer une fois pour avoir la vitesse de la crêpe, et une deuxième fois pour avoir la position de la crêpe. N'oublie pas les constantes d'intégration !

c'est ce que j'ai fait et à la fin je trouve y(t)=(1/2)gt²+v_0y

mais apres je me suis demandé si on devait considérer le moment ou la crepe monte puis celui ou elle descend ?

c'est faux désolé ! tu as fait correctement la première intégration mais pas la 2e

il manque un "-" devant le (1/2)gt² ?

oui entre autre mais il y a d'autres erreurs

vy = -gt + v0y

ensuite intégre correctement chaque membre, n'oublie pas les constantes

donc on a y(t) = -(1/2)gt²+v_oyt

et la constante d'intégration ?

+h nan ?

oui

ouf merci.
je vais pouvoir continuer l'exo maintenant et si j'ai d'autres questions sur les questions suivantes je les posterai

bon ben je sens que je suis pas arrivée au bout de mes peines je dois exprimer t_max nécessaire à la crêpe pour atteindre sa hauteur maximale h_max en fonction de v_yo et g.

pour le moment ce que je peux dire c'est que à tmax y(tmax)=hmax=-(1/2)gt²+v_yot+h
(et encore je suis même pas sûre que j'ai le droit de mettre ça) et apres ?
ou alors reprendre l'equation horaire et la dériver et a tmax vy est nulle donc je peut trouver tmax.

si une des deux solutions la bonne c'est laquelle ?

en fait j'opte pour la 2ème solution car j'arrive a une résultat cohérent mais je veux bien confirmation.

oui bien sûr il faut dériver et chercher quand la dérivée s'annule (donc quand la vitesse s'annule)

c'est bon j'ai reussi à terminer la premiere partie et maintenant j'attaque la seconde et la ça va être chaud je me souviens de rien !

voila j'ai un disque de rayon R qu'on lance vers le haut à partir d'une hauteur h avec une vitesse linéaire v_o de son centre de gravité et une vitesse angulaire _o autour d'un axe Oz
Le disque n'est soumis qu'à son poids

question : il faut démontrer que la vitesse angulaire du disque est constante au cours du mouvement.

j'ai pensé utiliser le théorème du moment cinétique d'un solide mais je ne sais plus l'utiliser depuis le temps,
je me souviens juste que L_o=OMdm
et dL_o/dt=M_Fext

mais voila je ne sais pas comment faire pour dériver L_o

*** message déplacé ***

est ce que tu as le moment d'inertie de ton disque car si oui et si il s'appelle J, alors
Lo=Jw
donc après tu dérive a J constant  et voila
sauf érreur...

*** message déplacé ***

on me dit juste que le moment d'inertie s'appel J₁ mais rien de plus

*** message déplacé ***

Bonjour,

extrait de la FAQ du forum :

Q04 - Où dois-je poster une nouvelle question ?

Pour poster un nouveau message, choisissez le forum correspondant à votre niveau : collège ou lycée ou supérieur.

Pour parler du site en général (forum, suggestions d'amélioration, problème rencontré avec une fonctionnalité, etc.) utilisez plutôt le forum site.

Il existe également des forums plus spécifiques : Autre, Détente, Expresso, Espace Profs, etc.

Une fois le bon forum trouvé, choisissez "Nouveau sujet" ou descendez sous la liste des messages pour avoir accès au formulaire " Poster un nouveau message ". Et remplissez soigneusement les différents champs en respectant les consignes de bon usage que vous pourrez trouver tout au long de la lecture de cette F.A.Q.