Inscription / Connexion Nouveau Sujet
Étude du mouvement d'un chariot
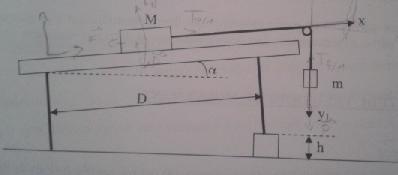
Bonjour, le système étudié est un chariot de masse M suspendu à une masse m, on considère le fil inextensible et on néglige les frottements dû à la poulie.
Soit x(t) le mouvement du chariot et y1(t) le mouvement de la masse.
Bilan des Forces extérieurs :, la tension exercées par le fil sur le chariot ;
, le poids du chariot ;
la réaction normale du support ;
, la force tangentielle du support ;
, la tension exercée par le fil sur la masse et
, le poids de la masse.
Voilà le problème, je bloque à une question qui demande d'écrire la relation entre x et y1 ; et
;
et
Dans des précédentes questions, on à défini que
M =
+
+
+
m =
+
Les normes de et
sont égales.
Il y a surement quelque chose qui m'échappe...
Toute aide sera la bienvenue 
D'avance merci
bonjour,
le fil est inextensible donc si M bouge de dx, m bouge de dy1= ...
tes relations sont incorrectes: un nombre ne peut pas être égal à un vecteur!
de plus la loi fondamentale est une relation vectorielle qui donne l'accélération, pas la vitesse: F = m a
ici, en projection, cela donne :
M x" = T+...
m y"1 = ...
"je bloque à une question qui demande d'écrire la relation entre x et y1 et ... "
x(t) = y1(t)
dx/dt = dy1/dt
d²x/dt² = d²y1/dt²
Faut pas chercher plus loin. (Avec, bien enetendu, le fil inextensible)
Sauf distraction. 
Merci pour ta réponse,
"loi fondamentale est une relation vectorielle qui donne l'accélération, pas la vitesse" Effectivement, erreur de recopie 
Si je comprend bien ta réponse, la norme de x(t) et égale à la norme de y1(t),
Mais après, je n'arrive pas à trouver la relation entre les vecteurs...
J'ai remplacé par la valeur des vecteurs, je trouve, si je ne me suis pas trompé,
Mx¨ = (T - sin( )*Mg - F )
)*Mg - F ) + (-cos(
 )*Mg + RN)
)*Mg + RN)
Or Le chariot ne bouge pas en ; donc (-cos(
 )*Mg + RN) = 0 ; donc -cos(
)*Mg + RN) = 0 ; donc -cos( )*Mg = RN
)*Mg = RN
Et my¨1 = ((mg + T)*cos( )
) + ((mg + T)*sin(
 )
) ...
Avec un vecteur unitaire ayant le sens et la direction de l'axe des x et
un vecteur unitaire ayant le sens et la direction de l'axe des y :
x. = y.
dx/dt . = dy/dt .
d²x/dt² . = d²y/dt² .
-----
M.d²x/dt² = T - P.sin(alpha) + Rn.cos(90°) - F
M.d²x/dt² = T - Mg.sin(alpha) - F
m.d²y1/dt² = P' - T'
m.d²y1/dt² = mg - T'
On a donc le système :
M.d²x/dt² = T - Mg.sin(alpha) - F
m.d²y1/dt² = mg - T'
et on sait que T = T' --->
M.d²x/dt² = T - Mg.sin(alpha) - F
m.d²y1/dt² = mg - T
On sait aussi que d²x/dt² = d²y1/dt² --->
M.d²x/dt² = T - Mg.sin(alpha) - F
m.d²x/dt² = mg - T
On élimine T entre les 2 équations :
M.d²x/dt² = mg - m.d²x/dt² - Mg.sin(alpha) - F
(M+m).d²x/dt² = mg - Mg.sin(alpha) - F
(Ceci en négligeant les influences du moment d'inertie de la poulie et de la masse du fil)
-----
Sauf distraction. 


