Inscription / Connexion Nouveau Sujet
Etude d'un vaisseau lunaire
Bonjour,
J'ai de nombreux soucis avec cet exercice.
L'énoncé : "On admettra que la Lune de centre O, de masse M, de rayon R est fixe par rapport à un référentiel galiléen. Un vaisseau spatial habité, de masse m, en provenance de la Terre (supposé à l'infini) arrive avec une vitesse vo au voisinage de la lune suivante une trajectoire hyperbolique dont l'asymptote est à la distance b du centre de la Lune. On admettra que le vaisseau n'est soumis qu'à l'attraction lunaire, soit a la distance d'approche minimale du vaisseau au centre de la Lune. On désigne par G la constante de gravitation universelle.
Données :
Rayon lunaire : R = 1740 km
Intensité de pesanteur à la surface de la Lune : g0 = 1.62m/s²
1) En appliquant les lois de conservation du moment cinétique d'une part, de l'énergie mécanique d'autre part :
a) établir la relation entre v0, b et a.
b) Calculer la vitesse initiale v0 nécessaire pour que l'ont ait b = 10R/3 et a = 2R
c) Quelle est alors la vitesse vA au point A de plus courte approche de la Lune ?"
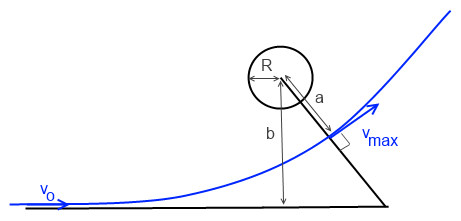
Déjà, le côté mathématique m'embête... Je ne comprends pas la phrase "dont l'asymptote est à la distance b du centre de la lune", ce qui fait que mon schéma n'est pas complet... J'ai bien le centre de la lune, la distance a qui apparaît, les deux asymptotes aussi et mon point M (le vaisseau) sur l'hyperbole.
Mon second soucis, plus physique, c'est pour le moment cinétique : Lo = OM  p (désolé mais je ne sais pas comment faire apparaître le vecteur.) avec p = mv et c'est là mon soucis : Comment exprimer v ?
p (désolé mais je ne sais pas comment faire apparaître le vecteur.) avec p = mv et c'est là mon soucis : Comment exprimer v ?
Ensuite, comme le vaisseau n'est soumis qu'à l'attraction lunaire, il n'est soumis qu'à la force : F = (-GMlm/OM²)*uom avec Ml qui est la masse de la lune. La force étant conservative, l'énergie mécanique se conserve Em = Ec + Ep avec Ep = -GMlm/r + C, en posant que r = OM.
Ec = mv²/2
Je retrouve mon problème, je ne sais pas exprimé la vitesse.
Et j'ai pu aller jusqu'à... Em(A) = Em(+ )
)
0 - GmMl/a = mv0² - GmMl/b
Le truc qui m'a montré que j'avais faux, en résolvant ça, pour avoir un lien entre a, b et v0, j'ai obtenu un carré négatif, pas possible.
Voilà. D'où, je pense ne pas savoir qu'est-ce que b. Et je ne sais pas comment travailler ce problème.
Merci d'avance pour l'aide.
re-bonsoir,
b est appelé "paramètre d'approche" (ou "d'impact"), càd la distance entre le centre de la Lune et l'asymptote à la trajectoire parabolique, tandis que a est la distante minimale entre le vaisseau et le centre de la Lune (donc correspondant à la vitesse maximale vmax du vaisseau). Un petit filon : lorsque le vaisseau est à la distance a de la Lune son vecteur vitesse, de norme vmax, est normal au rayon vecteur de norme a ; la norme de L0 est facile à écrire et sa conservation donne une relation entre v0 et vmax.
L'autre relation est obtenue en écrivant la conservation de l'énergie mécanique.
Cet exo n'est pas trop difficile, et quand j'en aurai fini avec ton pb d'électrostatique j'y regarderai ; mais je vois qu'il y a des ténors qui viennent d'arriver sur le forum, et à mon avis tu vas avoir la solution bien avant...
Merci pour vos réponses !
Je ne demandais pas plus qu'un dessin et une explication sur b, donc merci prbebo et krinn, j'avais dû mal à me représenter b et ça va mieux maintenant.
Donc avec le schéma, j'ai écrit la conservation du moment cinétique (en vérifiant déjà que dLo/dt = 0 (OM F) avec F = (-GMlm/OM²)*ur et OM = rur d'où Lo = cst.
F) avec F = (-GMlm/OM²)*ur et OM = rur d'où Lo = cst.
J'ai ensuite écrit que Lo (A) = Lo ( )
)
Donc que : aur mvmax = -buy
mvmax = -buy mvoux + 0
mvoux + 0
Ce qui donne que : a*m*vmax = b*m*v0
J'ai donc ensuite écrit la conservation de l'énergie mécanique (comme au premier poste)
Em(A) = Em( )
)
Ce qui donne : (mvmax²/2) - (GMm/a) = (mv0²/2) + 0
vmax² = vo² + GM/a
J'ai remplacé dans la première équation en l'élevant au carré : a²m²(vo² + GM/a) = b²m²vo²
Au final j'ai obtenu : vo² = (aGM)/(b²-a²)
Le soucis (^^) c'est que je ne colle pas avec les notations de les notations de l'énoncé (je n'ai ni go, ni R qui apparaît)
Bonsoir krinn,
meuh non je ne t'ai pas grillé, c'est juste que j'avais la flemme de faire le schéma et que j'ai attendu qu'on le fasse à ma place...(te fâche pas, c'est de l'humour de 11h du soir et c'est loin d'être le meilleur  )
)
OK pour la relation a.vmax = b.v0. On verra le reste demain.
Bonne fin de soirée à tous les deux. BB.
Bonjour à tous les deux,
je reprends le pilotage du vaisseau :
L = constante donne bien aVA = bV0, où vA = vmax (vaisseau au plus près de la surface lunaire).
Energie mécanique : E = mv2/2 - GMm/r en un point M quelconque de la trajectoire.
GM est le produit de la constante de gravitation G par la masse M de la Lune. L'énoncé ne les donne pas, mais on peut les obtenir par une voie détournée, sachant qu'à la surface de la Lune (r = R le rayon lunaire), on a GMm/R2 = mg, le poids de la masse m soumise au champ de pesanteur lunaire g ; soit MG = R2g.
A l'infini, E = mv2/2 ; à la distance r = a de la Lune, E = mvA2/2 - gR2m/a.
L'égalité donne vA2 - gR2/a = v02.
Avec b/a = 5/3 soit VA = 5V0/3, et a = 2R soit gR2/a = gR/2, on arrive à v02 = gR/[(5/3)2 - 1] qui fournit v0 = 1260 m.s-1.
Merci !
ça marche bien ! Je l'ai refait en perm et ça me fait bien ça ! Je n'y ai pensé qu'après pour le go. Mais en effet, cet exercice était bien plus simple que celui d'électrostatique xD
Merci à vous deux, encore !
Bonjour à tous les deux,
tant mieux TheoNott si tu as compris ce corrigé, mais ne crois pas que cet exercice soit plus facile que celui d'électrostatique ( [url]https://www.ilephysique.net/sujet-conducteur-a-l-equilibre-274371.html[/url pour krinn). Je les trouve aussi difficiles l'un que l'autre car il nécessitent, non seulement une connaissance et une compréhension du cours, mais aussi la maturité nécessaire pour exploiter les infos de ce cours en vue de résoudre un problème donné (eh oui... on n'est plus en TS...).
Krinn et moi t'attendons de pied ferme pour la suite de tes aventures en électrostatique. BB.
![]() Conducteur à l'équilibre pour krinn. Pour une fois que je fais pas un aperçu avant de balancer mon post...
Conducteur à l'équilibre pour krinn. Pour une fois que je fais pas un aperçu avant de balancer mon post...