1. c'est illisible
2. il est interdit de poster un scan de l'énoncé, la moindre des choses est de le recopier.

Oups désolé...

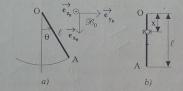
Une tige homogène de longueur l, de section négligeable et de masse m est suspendue à un axe horizontal (0,ez0) ( pivot sans frottement) par son extrémité O et peut osciller autour de O dans le plan (ex0,ey0) de la figure ci dessus.

Un anneau de petite dimension ( pouvant être considérée comme un point matériel ) et de même masse m ( figure ci dessus à droite ) est enfilé sur la tige et bloqué à la distance x de O.

1) Calculer le moment d'inertie du système {tige+anneau} par rapport à l'axe (O,ez0)

Pour cette question, j'en vient à dire que le moment d'inertie du système est égale à la somme des moments d'inertie des parties du système donc: I(Sstm)= (Ml²/3)+m.x²

2) Appliquer le PFD à ce système pour les moments au point O et en déduire l'équation du mouvement.

C'est ici que je bloque. J'écris donc mes actions mécanique extérieur:
-> Sstm = 2mgcosex0 - 2mgsiney0

Bati->Sstm = L.ex0 + M.ey0 + O.ez0    ( car pas de frottement )

Mais quand vient le moment d'exprimer le moment: Mo( ext->Sstm )= OGP + L.ex0+M.ey0

Je ne sais pas comment définir le point G centre de gravité de mon système.

Quelqu'un pourrait-il me venir en aide?

Et encore toutes mes excuses pour le manque de politesse.

Personne ?

Bonjour,

tu écris les moments des 2 poids séparément :
J d2theta/dt2 = ( M g (L/2) + m x ) sin (theta)
la réaction à l'axe ayant un moment nul