Inscription / Connexion Nouveau Sujet
Etude d'un mouvement
Bonjour, je viens vers vous avec un problème de mécanique, voici l'énoncé :
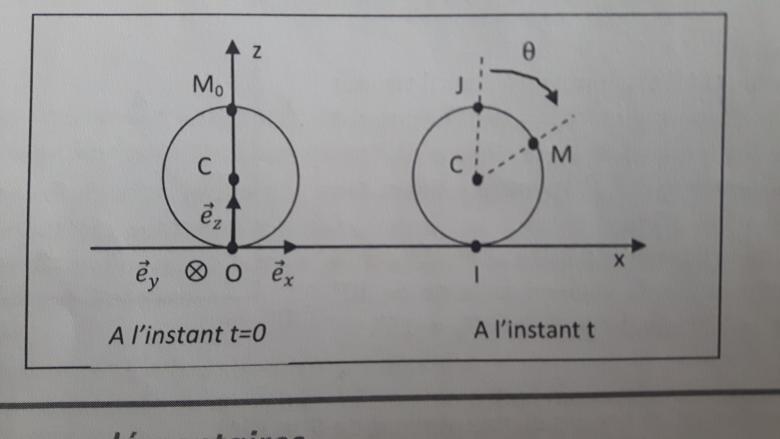
Une roue de rayon R et de centre C roule sans glissement sur un axe (Ox) avec une vitesse angulaire 
constante, tout en restant dans le plan (xOz). On se propose d'étudier le mouvement d'un clou planté dans la roue. A l'instant t = 0, M se situe en M0 de coordonnées x = 0, z = 2R. Les mouvements sont étudiés dans le référentiel fixe R associé au repère (O, ex,ey,ez)
1. Déterminer le sens et la direction du vecteur vitesse angulaire .
2. Comment s'exprimer la condition de non glissement
- Pour la question 1, je connais la différence entre sens et direction, mais je n'ai jamais su ce que représentait un vecteur de vitesse angulaire, et donc je ne vois pas comment déterminer son sens et sa direction
- Pour la question 2, j'ai donné une réponse mais je n'en suis pas certain, alors je vous la donne : La condition de non glissement implique que l'accélération est nulle, donc a = 0
Il y d'autres questions ensuite mais je vais essayer de répondre seul.
(Vecteur en gras)
Merci d'avance pour votre aide
AR2
Bonjour,
Merci, c'était en effet le moyen le plus logique de comprendre !
Et est ce que vous pourriez me conseiller pour la question 2 ?
Merci d'avance
AR2
Bonsoir
Appelons A le point de la roue en contact avec le sol à un instant donné.
La vitesse de glissement de la roue est alors par définition
(A)/R
Et il y a non- glissement si = ...
Bonjour,
Je ne sais pas vraiment quoi répondre...
Mais je dirais que V = Constante
Car V ne peut pas être égale à 0 car la roue est en mouvement...
Je pense
Merci d'avance de votre réponse
AR2
Attention c'est V(C) /R qui est non nulle (et constante)
Mais V(À)/R est bien nulle s il n'y a pas glissement en A
Si on écrit cette condition on trouve une relation du genre : v = R
V étant la vitesse de C dans R
Bonsoir,
Merci, j'ai bien compris ce que le non glissement représenter !
J'ai une question dans l'exercice qui porte sur le point C :
Déterminer les coordonnées Xc et Zc du point C à l'instant t en fonction de et R
Je n'arrive pas à répondre à la question vu que le point C est en mouvement rectiligne uniforme, etant donné qu'il s'agit du centre de la roue donc je ne sais pas comment trouver ces expressions
Merci d'avance
AR2
Ma réponse à la question est la suivante :
Xc = t
Mais pour Zc je ne sais... Le point C est placé à une hauteur R mais je ne vois pas comment me servir de
Dans R
C a pour coordonnées (xc,zc)
zc = R = Cste
V(C)/R = x'c ex
Avec x'c= dxc/dt
Appelons R1 le référentiel lié au centre de la roue et en translation par rapport à R, cad associé au repère (C,ex,ey,ez)
On a par composition des vitesses:
V(I)/R= V(C)/R + V(I)/R1
= x'c ex - Rw ex
Donc la condition de non glissement en I s'écrit:
x'c = Rw
Donc xc = ....
Xc = t est une horreur en physique car ce n'est pas homogène!
(Une distance ne peut pas être égale à un temps )
Xc = R.t
Merci. La question d'après porte sur le point M
Est ce que je dois effectuer la même méthode ?
Pardon...
C'est exactement la même que pour le point C
Déterminer les coordonnées XM et ZM du point M à l'instant t, en fonction de et R
J'ai déjà écrit que Z M = 2R
Et pour XM je dois me servir de l'angle 
Annuler
connectez vous