Quel est l'énoncé complet ?

Je parierais qu'il y a une erreur de signe dans l'équation différentielle que tu donnes.

non mais en fait j'ai un circuit ou j'ai trouvé l'équation différentielle :
E=RCd(s(t))/dt + s(t)
donc en effet j'avais mal réecrit mon équation différentielle

C'est déjà plus plausible.

E = RC d(s(t))/dt + s(t)

Je suppose que E est une tension continue permanente.

a)
Solutions de RC ds/dt + s = 0:
s = A.e^(-t/(RC)) avec A une constante réelle.

b)
Solution particulière de E = RC d(s(t))/dt + s(t) :
s = E

c)
Solutions générales de E = RC d(s(t))/dt + s(t) :

s(t) = E + A.e^(-t/(RC))

Si s(0) = 0, alors :
0 = E + A.1
A = -E, et on arrive finelement à :

s(t) = E(1 - e^(-t/(RC)))
-----
Sauf distraction.  

merci beaucoup ! on me demande ensuite l'allure de s(t) l s'agit de celle d'une exponentielle ?

j'ai ensuite ce circuit ou je dois trouver l'equation différentielle a laquelle satisfait s(t)

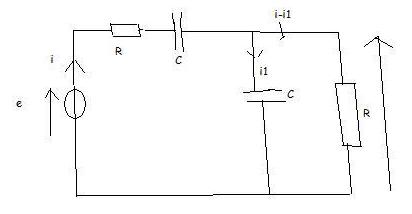[/url]

Edit Coll : image placée sur le serveur de l' (et recadrée). Merci d'en faire autant la prochaine fois ! [lien]    

je ne vois pas comment trouver l'equation différentielle a laquelle satisfait s(t) ...

Réponse au message du 28-10-08 à 20:45

Une manière parmi plein d'autres :

z2 = R // C
z2 = (R/(jwC))/(R + 1/(jwC)) = R/(1 + jwRC)

z1 = R en série avec C
z1 = R + 1/(jwC) = (1 + jwRC)/(jwC)

s/z2 = e/(z1+z2)

s/e = z2/(z1+z2)

s/e = (R/(1 + jwRC)) / [R/(1 + jwRC) + (1 + jwRC)/(jwC)]

s/e = jwRC/[jwRC + (1 + jwRC)²]

s/e = jwRC/(1 + j²w²R²C² + 3jwRC)

s*(1 + j²w²R²C² + 3jwRC) = jwRC.e

s + R²C² d²s/dt² + 3RC ds/dt = RC de/dt

R²C² d²s/dt² + 3RC ds/dt + s = RC de/dt
-----
Sauf distraction.  Vérifie

je ne comprend pas du tout ta manière moi je comptais faire avec loi des mailles loi des noeuds puis avec les transformées de laplace mais je n'aboutis pas

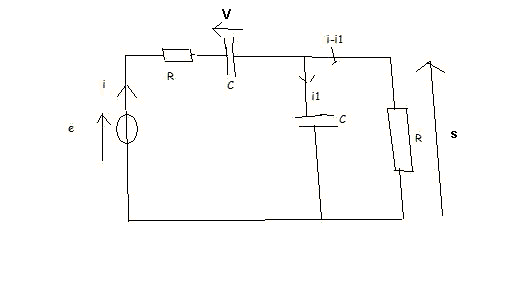
e = Ri + V + s
i = C. dV/dt
i1 = C.ds/dt
s = R(i - i1)

on élimine i1 de ce système:

e = Ri + V + s
i = C. dV/dt
s = R(i - C.ds/dt)

On élimine i de ce système :

e = RC. dV/dt + V + s
s = R(C. dV/dt - C.ds/dt)

e = RC. dV/dt + V + s
s = RC(dV/dt - ds/dt)

RC. dV/dt = e - V - s
s = e - V - s - RC ds/dt

V = e - 2s - RC ds/dt
dV/dt = de/dt - 2 ds/dt - RC d²s/dt²

e = RC. dV/dt + V + s
e = RC. (de/dt - 2 ds/dt - RC d²s/dt²)  + e - 2s - RC ds/dt + s

0 = RC. (de/dt - 2 ds/dt - RC d²s/dt²)  - 2s - RC ds/dt + s

R²C² d²s/dt² + 3RC ds/dt + s = RC de/dt
-----
Sauf distraction.  

merci !
pour terminer je dois donner l'expression de s(t) les condensateurs ne sont pas chargés à t=0

Pour déterminer l'expression de s(t), il faut connaître celle de e(t).

:-

je ne la connais pas ... elle n'est pas donnée

Je vais supposer que e est une tension continue permanente E, mais c'est une supposition gratuite.

R²C² d²s/dt² + 3RC ds/dt + s = RC de/dt
R²C² d²s/dt² + 3RC ds/dt + s = 0

p²R²C² + 3RCp + 1 = 0
p = (-3RC +/- V(9R²C²-4R²C²)]/(2R²C²)

p = (-3 +/- V5)/(2RC)

s(t) = A.e^[(-3-V5).t/(2RC)] + B.e^[(-3+V5).t/(2RC)]

s(0) = 0 --> A+B = 0 et donc A = -B

i1(t) = C.ds/dt
i1(t) = C.[A((-3-V5)/(2RC))e^((-3-V5).t/(2RC)) + B((-3+V5)/(2RC))e^((-3+V5).t/(2RC))]

i1(0) = E/R
C.[A((-3-V5)/(2RC)) + B((-3+V5)/(2RC))] = E/R
A(-3-V5)/2 + B(-3+V5)/2 = E

A(-3-V5)/2 -A.(-3+V5)/2 = E
A(-3-V5) -A.(-3+V5) = 2E
-V5 A = E
A = -(1/V5).E
B = (1/V5).E

s(t) = (E/V5).[e^((-3+V5).t/(2RC)) - e^((-3-V5).t/(2RC))]



-----
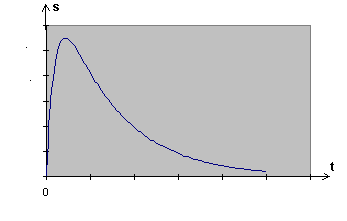
Calculs à vérifier.  

merci beaucoup !