Inscription / Connexion Nouveau Sujet
Etude d'un barrage
Bonjour,
Je travaillais des exercices de thermodynamique , et j'ai trouvé des difficultés dans la compréhension et la résolution d'un exercice portant sur l'étude d'un barrage.
Je présente le problème : D'abord le référentiel terrestre est supposé galiléen. Le barrage est formé d'un solide indéformable, en forme de pentaèdre de base rectangulaire. Sa section est un triangle isocèle, de hauteur , de demi-angle au sommet
. Sa masse volumique est
. Il est posé sur le sol horizontal et permet de retenir l'eau d'un lac dont la masse volumique est
. On suppose que les seules forces qui interviennent sont liées à la pression des fluides (eau et air), au poids du barrage et aux forces de contact exercées par le sol. La longueur
du barrage est suffisamment grande pour que l'on puisse négliger les forces de liaison intervenant à ses extrémités. On appelle
la pression uniforme de l'air au voisinage du barrage.
Dans un premier temps on a supposé que ni l'eau ni l'air ne peuvent s'infilter sous le barrage , dans ce cas on trouve que la force exercée par l'eau sur la face immergée est : et la force exercée par l'air sur la face non immergée :
, on trouve aussi (puisque le barrage est en équilibre ) que les composantes de la force de frottement solide normales et tangentielles sont respectivement : et
, et on en déduit la valeur minimale du coefficient de frottement pour que le barrage reste en équilibre sur le sol sans glisser :
Pour certaines valeurs données on trouve
On me demande ce qu'il se passera si l'air peut s'infiltrer sous le barrage et exercer une pression sur la base , et de donner la nouvelle valeur limite du coefficient de frottement f . Bon je calcule la nouvelle valeur de
et la nouvelle valeur du coefficient de frottement f et je trouve
, donc même si l'air peut s'infiltrer sous le barrage , ce dernier ne glissera pas et restera en équilibre .
A partir de là j'ai des difficultès , on me demande ce qu'il se passera si l'eau peut s'infiltrer sous le barrage. Je me dit que je ferai les mêmes calculs que pour l'air et je trouve f donc le barrage glissera. Mais quand je reviens voir le corrigé , ils ont ajoutés quelques lignes qui m'intriguent : " Si l'eau peut pénétrer sous le barrage, elle exercera une pression
sur la surface de la base. Cela crée une contribution en moins dans N. " Je n'ai pas compris pourquoi le " en moins " . Je m'explique : 1)Dans le calcul de la force appliquée par l'eau sur la base , on a le vecteur normal à la surface , qui est
, donc la force n'ajoutera une contribution qu'à N . 2) On suppose qu'il y'a une contribution dans T , alors si elle venait à diminuer sa valeur alors on aura
Je peux, si demandé, donner les questions telles qu'elles sont écrites et préciser mes calculs.
J'espère que vous pourrez m'aider à déchiffrer cette ambiguité.
Merci d'avance pour toute aide ^^
Bonjour
Cela crée une contribution en moins dans N. " Je n'ai pas compris pourquoi le " en moins "
Pour que le barrage se mette à glisser, il faut :
T >fs.N
avec fs : coefficient de frottement statique.
En absence d'infiltration, tu dois obtenir (je n'ai pas fait les calculs...) :
T<fs.N avec N : réaction normale en absence totale d'infiltration.
En présence d'infiltration d'air, la projection des différentes forces sur un axe vertical doit te conduire à trouver une nouvelle valeur N' de la réaction normale :
N'=N-PoS où S est l'aire de la base du barrage , puisque l'air exerce sur le barrage une force verticale vers le haut d'intensité Po.S
La valeur de T est inchangé. J'imagine que l'on obtient l'inégalité
T
fS.N'
En cas d'infiltration d'eau, la force verticale ascendante exercée par l'eau sur la base a pour intensité :
(Po+
.g.h).S .
La condition d'équilibre vertical du barrage va te conduire à trouver une nouvelle réaction normale :
N"=N- (Po+
.g.h).S
La valeur de T étant toujours la même, on obtient j'imagine maintenant :
T>fs.N"
Le barrage glisse...
Evidemment, le modèle est assez grossier s'il s'agit de considérer fs comme une constante, qu'il y ait infiltration ou pas.
Dans le calcul de N (sans eau ni air sous le barrage), on tient compte du poids du barrage et de la composante verticale de la force due à la pression hydrostatique de l'eau sur le coté mouillé du barrage et de la composante verticale de la force due à la pression d'air sur les 2 cotés du barrage.
Toutes ces forces ont le même sens.
Si l'eau et l'air peuvent pénétrer sous le barrage, il faut en plus tenir compte de la poussée verticale vers le haut sur le barrage due à cette présence d'eau et d'air sous le barrage.
... et celle poussée est de sens opposé à toutes les forces mentionnées avant.
Sauf distraction. 
Bonsoir,
Je tiens à vous remercier pour vos réponses vanoise et J-P . Mais je ne comprend pas une nouvelle chose, l'importance du dans nos conclusions ( puisque
, rien ne nous indique que pour une valeur donnée de
on a avait glissement ou non selon l'inégalité
)
Et de plus dans le dernier calcul de , on a bien N"=N-(P0+
gh).S , mais pour T , si on considère la viscosité de l'eau , on peut avoir T'=T-f < T , et dans ce cas on aura une autre valeur et par la même occasion une autre conclusion ( même si je ne sais d'où ils tirent leurs conclusions en se basant sur )
Je joint un dessin pour mieux comprendre le schéma de l'exercice.
Merci d'avance ^^
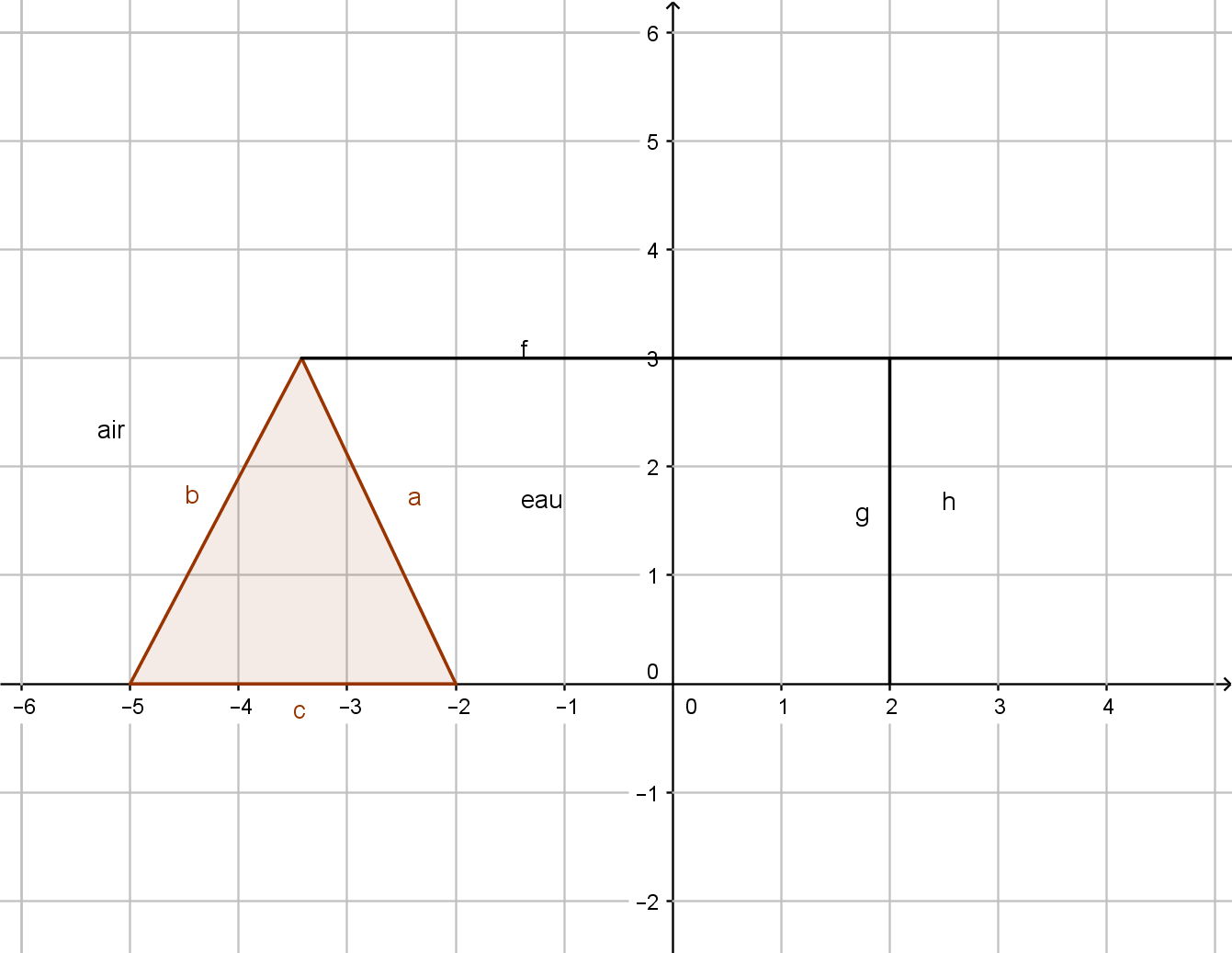
N'ayant pas l'énoncé complet, difficile d'être catégorique. Une façon de voir les choses peut être la suivante :
T est ici fixe ; on peut aussi imaginer fs fixe et considérer la réaction normale comme variant en fonction des infiltrations... cette réaction prenant les valeur N (sans infiltration), N' (infiltration air), N" (infiltration eau).
Il suffit alors de comparer T à fs.N, à fs.N' puis à fs.N" pour savoir s'il y a glissement ou pas. Les commentaires de ton corrigé sur l'influence des infiltrations sur la réaction normale me poussent à penser qu'il s'agit de ce que demande le concepteur du problème. La notion de fs(min) n'a pas vraiment de sens dans ce cas. Evidemment, comme déjà dit, supposer fs comme une constante malgré les infiltrations est une modélisation grossières.
Une autre approche, à mon avis plus réaliste, consiste à considérer T et N comme deux constantes et fs comme une grandeur dépendant des états de surface à la base du barrage. On peut alors définir une valeur minimale du coefficient de frottement statique mais je ne vois pas comment ensuite déterminer les valeurs de fs suivant la présence ou nom d'infiltrations même s'il est intuitivement évident que fs diminue en présence d'infiltrations. Cette méthode ne semble pas celle demandée ici...
Bonsoir,
Je pourrai poster l'énoncé et le corrigé complets, seulement je ne sais pas si j'en ai le droit ( il n'y a aucune publicité dans mes images , ou des références sur l'auteur ou nom du livre ... mais je pense que sa me demandera 4 posts d'image ^^'' ) . Vous pouvez m'expliquer comment on peut comparer T à fs.N ( respectivement N' et N" ) car à ce que je sache fs ne peut se calculer qu'expérimentalement non ? Et ceci dépend de la nature des surfaces de contact. Pouvez-vous m'expliquer aussi pourquoi vous pensez que l'énoncé considére fs comme constante ? Et aussi comment dans la seconde approche on peut considérer T et N comme constantes, car si l'eau ou l'air s'infiltre on doit considérer de nouvelles forces et donc les expressions de T et N changeront :/
Je m'excuse pour ces questions
Merci d'avance
J'ai peut-être (???) compris ton problème en relisant ta phrase :
et on en déduit la valeur minimale du coefficient de frottement pour que le barrage reste en équilibre sur le sol sans glisser :
Tu n'as peut-être pas très bien compris la loi de Coulomb sur les frottements solides.
Tu sembles appeler systématiquement fmin le rapport (T/N) ou (T/N') ou (T/N").
Tu peux calculer ce rapport si tu veux dans les trois cas mais il ne s'agit pas d'un coefficient de frottement mais d'un simple rapport de deux forces qu'il vaudrait mieux désigner par une autre lettre "r" par exemple. Dans ces conditions, la loi de Coulomb sur les frottements solide peut s'écrire :
Absence de glissement si :
r
fs où fs est le coefficient de frottement statique. Ce coefficient dépend comme tu l'as dit des états de surface et se détermine expérimentalement : il ne se calcule pas. J'imagine qu'il est fourni par l'énoncé.
Sans nécessairement fournir un énoncé complet, tu pourrais au moins préciser les hypothèses faites dans ce problème sur le coefficient de frottement statique...
Bonjour,
A part les hypothèses énoncées au début , il y'a celles-ci :" On admet que ni l'air, ni l'eau ne peuvent pénétrer sous le barrage. On considère que ce dernier ne tient alors en équilibre sur le sol que par l'action de la force de frottement solide. Dans ce cas la réaction du sol sur le barrage est représentée par : une composante normale N verticale ascendante et une composante tangentielle T horizontale qui s'oppose au glissement du barrage. L'équilibre statique n'est garanti que si Tf.N , expression dans laquelle f est un coefficient constant, appelé coefficient de frottement statique du barrage sur le sol. "
Après la détermination des forces T et N ( sans infilration ni d'air ni d'eau ) il est demandé de déduire la valeur minimale du coefficient de frottement, pour que le barrage reste en équilibre sur le sol, sans glisser. Le correcteur à répondu de cette manière: Pour qu'il n'y ait pas glissement, il faut Tf.N ; fmin=T/N , et on en a déduit l'expression et la valeur.
Il y'a aussi une question , je ne sais si elle aide dans la détermination de la situation du barrage : Montrer que si 
+
>
/2 alors le barrage reste en équilibre . Où tan()=f
D'accord avec le contenu de ton dernier message sauf avec cette partie de phrase de ton corrigé (en rouge) que je trouve maladroite et qui, je pense, t'a induit en erreur :
Pour qu'il n'y ait pas glissement, il faut T
f.N ; fmin=T/N , et on en a déduit l'expression et la valeur. Puisque T et f sont considérés comme deux constantes (l'énoncé est explicite à propos de f, ce qui est une approximation comme on en fait toujours dans les modélisations), il est plus correct d'écrire :
Absence de glissement si N
T/f
L'inégalité est satisfaite sans infiltration puis avec infiltration d'air :
N
T/f ; N'T/f
Elle n'est pas satisfaite si infiltration d'eau :
N"<T/f
Cela conforte mes message précédent ; j'ai juste appelé fs plutôt que f le coefficient de frottement statique.
Bonsoir,
Merci pour votre réponse ceci m'éclaircit un peu. Mais j'ai quelques question s'il vous plait : dans le corrige ( ni dans les question d'ailleurs ) il n'a jamais été question de comparer les valeurs de N à T/f . Pour cela je ne vois comment ils ont pu trancher pour la dernière conclusion ( le barrage glisse si il y'a infiltration d'eau car fmin=1 et c'est une situation critique ) . Et aussi, je comprend que T fut considérée constante , mais dans la dernière question , ils ont indiqué ce " au moins " donc , selon le corrigé , on a glissement meme si on ne considère pas la force qui pourrait s'ajouter autre part qu'à N , c'est à dire à T , non ?
Merci d'avance et je m'excuse pour toutes ces questions :/
J'ai bien l'impression que tu manipules des choses apprises par coeur mais non vraiment comprises.
Approche théorique générale.
A)
Cas où l'eau et l'air ne peuvent pas pénétrer sous le mur.
On calcule la composante verticale de toutes les forces appliquées au barrage, soit :
a) Le poids du "mur" : On trouve Poids = Lh².Rho*g*tan(alpha) (verticale vers le bas)
b) La composante verticale de la force exercée par l'air et l'eau sur le "mur", on trouve F1 = (2Po.h + mu*g.h²/2)*L*tan(alpha) (verticale vers le bas)
c) Raction du sol sur le mur (verticale vers le haut)
Comme le mur ne bouge pas en vertical, la somme algébrique des 3 forces ci-dessus est nulle et on a donc :
|N| = Lh².Rho*g*tan(alpha) + (2Po.h + mu*g.h²/2)*L*tan(alpha) (N est vertical vers le haut)
qu'on peut écrire aussi : |N| = (2Po/(gh) + Rho + mu/2) * L.h².tan(alpha).g
*****
On calcule la composante horizontale de toutes les forces appliquées au barrage (qu'on note T) ... et on trouve ;
T = mu/2 * LH² * g (horizontale de droite vers la gauche sur ton dessin)
*****
Si le coefficient de frottement statique entre le mur du barrage et le sol où il repose est noté f, on aura ceci :
Si T > f * N la barrage glissera
Si T < f * N ne barrage ne glissera pas.
Pour que le barrage ne glisse pas, il faut donc que f > T/N
Donc la valeur min de f pour que le barrage ne glisse pas est : fmin = T/N
Pour vérifier si le barrage glisse ou non, il faut faire les calculs numériques à partir des données numériques (que tu n'as pas fourni ici)
On calcule la valeur numérique de N = (2Po/(gh) + Rho + mu/2) * L.h².tan(alpha).g = ...
On calcule la valeur numérique de T = mu/2 * LH² * g = ...
On calcule ensuite la valeur numérique de T/N = ...
On doit ensuite vérifier si la valeur numérique calculée de T/N est > ou < que la valeur de f (coeff de frottement entre le mur du barrage et le sol qui le supporte) (qui doit aussi être donnée)
... et enfin pouvoir conclure en fonction du résultat de cette dernière opération si le barrage glisse ou ne glisse pas.
********************
B)
On recommence les mêmes opérations que ci dessus ... mais dans le cas où l'eau et l'air peuvent s'infiltrer entre le mur du barrage et le sol qui le supporte.
Tous les calculs sont identiques à ceci près, qu'il faut en plus tenir compte dans le calcul de la composante verticale de toutes les forces appliquées au barrage ... de la force verticale vers le haut due à cette infiltration.
... donc on finit par trouver une valeur de N inférieure ici à celle trouvée dans le cas A (alors que la force T horizontale reste la même)
Et donc on aura aussi un rapport T/N plus grand ici que dans le cas A... et il est alors bien possible (il faut faire les calculs numériques) qu'on arrive maintenant à T/N > f et que le barrage glisse (même si il ne glissait pas dans le cas A)
Médite cela...
Sauf distraction.
Bonjour,
Je vous remercie pour votre réponse. Je vous ai parfaitement compris . Sauf que l'énoncé ne fournit aucune valeur de f :/ , et après calcul de fmin dans le cas où l'eau s'infiltre sous le barrage ils ont conclut que la situation est critique et que le barrage peut glisser .
Mais maintenant que j'ai bien compris , je pense que c'était juste une maladresse de la part du correcteur.
Sinon , le " au moins " peut être fait penser à l'existence d'une force tangentielle ( une force de viscosité peut-être ? ) dont ils n'ont pas tenu compte car fmin restera supérieure à 1 et que la situation restera critique ( selon eux , pour ma part j'ai bien compris qu'il faut comparer T/N à f ^^ ) ?
Merci pour toutes vos réponses vanoise et J-P .
Annuler
connectez vous