Inscription / Connexion Nouveau Sujet
Équivalence Thévenin-Norton
Bonjour.
Je dispose de l'énoncé suivant :
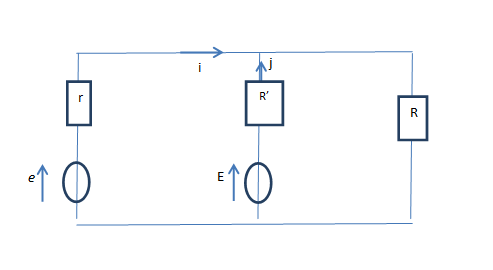
"Calculer i et j en fonction de e en utilisant les équivalences Thévenin/Norton. (Exceptionnellement on pourra, pour alléger le calcul, utiliser directement les valeurs numériques de r, R', R et E sans passer par une formulation entièrement littérale). "
Données : r=2 , R=R'=10
, R=R'=10 et E=10V, mais e non connu.
et E=10V, mais e non connu.
Je ne vois pas comment faire avec les équivalences Thévenin/Norton... Avec les lois de Kirchhoff, je trouve :
i=(e-5)/7
j= (-6/7)*((e/12)-1)
Est-ce quelqu'un trouve le même résultat ? Et peut aussi m'aider pour les équivalences Thévenin/Norton en m'indiquant la procédure à suivre SVP ?
Merci d'avance à celles et ceux qui prendront la peine de m'aider 
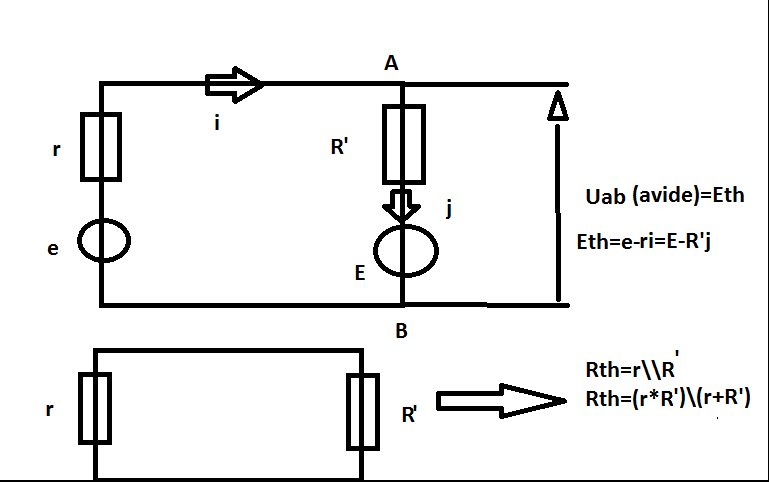
bonjour voila la procédure pour le théoreme de thévenin :
il consiste a calculer dabord Eth(la tension du thévnin a vide )
aprés tu calculer la résistece de thévnein ( résistence équivalente )
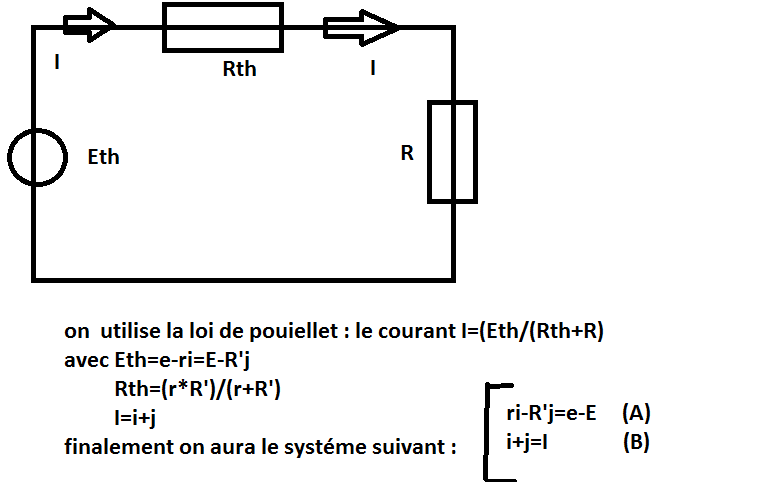
finalement on a aboutie a un systéme de 2 équation dont la résolution vous donne l'éxpersion des courants i et j en fonction de r R' E et e
Merci beaucoup de m'avoir expliqué le théorème de Thévenin ! J'avais finalement trouvé une autre technique qui s'apparente beaucoup à la votre : par les équivalences Thévenin-Norton, je retombe sur une association en série d'une source de tension (e/r + E/R') * Req et d'une résistance Req comme dipôle actif, puis en appliquant la loi de Kirschhoff, je trouve une expression de i+j. Avec cette expression, j'applique la loi des mailles dans les deux mailles du circuit initial contenant i et i+j d'une part, et j et i+j d'autre part, pour finalement retomber sur les expressions de i et de j que j'ai trouvées auparavant.
Votre raisonnement m'apporte un nouveau point de vue à adopter sur la résolution de ce genre d'exercices.
Donc merci beaucoup à vous d'avoir pris le temps de m'aider pour cet exercice !