Inscription / Connexion Nouveau Sujet
Equilibre d'un cylindre dans une coquille
Bonjour,
J'ai trouvé quelques difficultés en travaillant des problèmes de mécanique du solide. Mais je bute sur la dernière partie ( toutes les parties sont indépendantes car le problème a pour but d'étudier diffèrents mouvements d'un cylindre creux dans diffèrentes situations ) . J'espère que vous pourrez m'aider à avancer.
J'arrive en appliquant le théorème du moment cinétique respectivement au cylindre au point I ( point de contact entre le cylindre et la coquille ) puis au cylindre+coquille+barre au point  dans le référentiel R :
dans le référentiel R :  =
= et
et
Il est évident que  =0 est une solution quelque soit la valeur du facteur
=0 est une solution quelque soit la valeur du facteur . Mais pour la deuxième valeur de
 , je me demande même si cela est possible d'écrire la solution en utilisant les fonctions usuelles.
, je me demande même si cela est possible d'écrire la solution en utilisant les fonctions usuelles.
J'essaye d'avoir des conditions sur le facteur : il faut que :
( on peut considérer que
 est toujours positive ) mais là je bloque.
est toujours positive ) mais là je bloque.
J'ai aussi essayé de dessiner un graphe ( que je joint dans un deuxième post puisqu'on ne peut attacher qu'une seule image par post ) pour voir les intersections possibles entre la fonction sin et
et
J'espère que vous pourrez m'aider afin de continuer cette dernière partie et mieux profiter du problème.
Merci d'avance .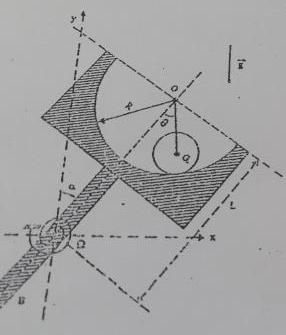
***Image recadrée***
Voici le graphe qui montre quelques intersections , mais cela ne m'avance pas grandement.
Je peux poster tout le problème si besoin mais les parties sont indépendantes.
Je m'excuse du double post.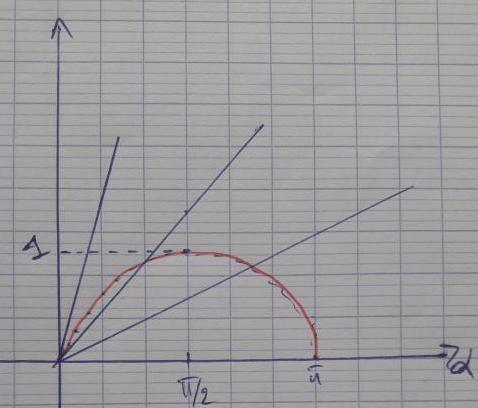
***Image recadrée***
Bonsoir
C'est bien d'expliquer ce que tu as fait et tes difficultés mais il est difficile de t'aider sans connaître l'énoncé de façon précise...
Bonjour , en fait j'avais pris l'énoncé dans la photo mais la photo a été recadrée ce qui a exclu l'énoncé. Je viens de m'en rendre compte je m'excuse .
J'écris l'énoncé : La demi-coquille est rigidement solidarisée d'une barre massive de sorte que son axe, contenant O , soit dans le plan de symétrie transverse de l'ensemble. Le centre d'inertie du dit ensemble est  et on note L la distance
et on note L la distance  O . Au point
O . Au point  est fixé un ressort de rappel linéaire de constante k fournissant un couple de moment
est fixé un ressort de rappel linéaire de constante k fournissant un couple de moment  =-k
=-k , où
, où  désigne l'angle que forme la barre avec la verticale ascendante. Le cylindre est placé dans la demi-coquille et on s'intéresse aux équilibres possibles du système ainsi constitué placé dans le champ de pesanteur g.
désigne l'angle que forme la barre avec la verticale ascendante. Le cylindre est placé dans la demi-coquille et on s'intéresse aux équilibres possibles du système ainsi constitué placé dans le champ de pesanteur g.
1) Établir en appliquant le théorème du moment cinétique la condition d'équilibre statique du sytème. ( fait )
2) Montrer que l'équilibre est possible pour deux valeurs de  que l'on précisera. Et décrire, en fonction des valeurs du facteur k/mgL les différentes situations envisageables.
que l'on précisera. Et décrire, en fonction des valeurs du facteur k/mgL les différentes situations envisageables.
3) Le système, supposé initialement immobilisé en 
 0 est libéré. Discuter alors de la stabilité des équilibres possibles en fonction des situations ci-dessus et de la valeur initiale
0 est libéré. Discuter alors de la stabilité des équilibres possibles en fonction des situations ci-dessus et de la valeur initiale  0 choisie.
0 choisie.
Je n'en suis qu'à la deuxième question. Je ne vois pas comment d'abord trouver la deuxième valeur de l'angle avant de pouvoir décrire.
Merci d'avance.
Bonsoir
Tu évoques des fonctions mathématiques utiles ici. Je ne sais pas si tu as déjà eu un cours sur la diffraction de la lumière. Si oui: la fonction "sinus cardinal " doit être familière. Si non: renseigne toi sur la fonction telle que:
f (x)=sin (x)/x .
Remarque: l'étude des positions et de la nature des positions d'équilibre serait sans doute plus simple en raisonnant sur les extrema d'énergie potentielle. Ce problème présente des analogies avec l'étude du métronome...
Bonsoir,
Je vous remercie pour votre réponse. Je me suis renseigné sur la fonction sinus cardinal. Et j'ai repensé au sujet. En fait si on exclu la solution évident  =0. La problème revient à trouver des conditions sur
=0. La problème revient à trouver des conditions sur pour avoir une seconde solution. J'ai tracé la fonction sur un calculateur et je joint l'image. On a l'angle
 varie ( dans le problème ) entre 0 et 2
varie ( dans le problème ) entre 0 et 2 . Et en tracant la droite y=b on voit directement qu'on a intersection tant que b
. Et en tracant la droite y=b on voit directement qu'on a intersection tant que b 1.
1.
Sinon je ne vois pas à partir de ces informations quels situations décrire. On a pour b>1 une seule solution qui est 0 . Et pour b 1 deux solutions , 0 et une autre dont je n'ai pas trouvé d'expression ni sur l'internet ni par l'effort personnel.
1 deux solutions , 0 et une autre dont je n'ai pas trouvé d'expression ni sur l'internet ni par l'effort personnel.
Et pour la dernière question, à propos des énergies potentielles. J'aimerai demander si ce ressort spiral applique une force ou seulement un couple ( pour voir si j'inclus l'énergie potentielle de sa force ou non)
Merci d'avance
PS :La courbe du sinus cardinal rencontre l'axe des abscisses en  et 2
et 2 .
.
Le ressort spiral exerce un couple.
En écrivant l'expression générale de la différentielle de l'énergie potentielle :
On obtient, à une constante arbitraire près que l'on peut choisir nulle, une énergie potentielle élastique :
Envisageons une position d'équilibre telle que :
La représentation graphique que tu as faite du sinuscardinal montre que la condition précédente n'est valide que b<1. Il faut donc envisager deux cas :
Premier cas : : une seule position d'équilibre possible :
. Cette position est stable, elle correspond à un ressort spiral très “raide”.
Second cas : b<1 (ressort spiral plus “mou”) : trois positions d'équilibres possibles :
la position qui maintenant est instable ; les deux positions stables symétriques qui correspondent à l'intersection de l'horizontale y = b avec la courbe d'équation
.
Remarque : je ne sais pas si l'énoncé envisage l'éventualité suivante : si b est suffisamment faible pour que cette intersection corresponde à des valeurs telles que : , le cylindre tombe de la demie coquille...
Comme déjà dit, tout cela est beaucoup plus simple en raisonnant sur l'énergie potentielle.
Bonsoir,
Pour l'énergie potentielle de pensanteur je ne vois pas comment l'exprimer. Je pense à déterminer le centre de gravité du système {cylindre+coquille+barre} et ensuite essayer de trouver une relation entre  et la cordonnée suivant y de ce centre de gravité. Le problème est la masse totale du système qui n'est pas donnée.
et la cordonnée suivant y de ce centre de gravité. Le problème est la masse totale du système qui n'est pas donnée.
J'espère que vous pourrez m'aider afin d'avancer.
Merci d'avance
Le centre d'inertie du dit ensemble est

Cette phrase simplifie énormément la situation puisqu'on peut considérer, dans ce contexte, que le centre de gravité se confond avec le centre d'inertie. Seules l'énergie potentielle de pesanteur du cylindre et l'énergie potentielle élastique du ressort sont susceptibles de varier dans ce problème !
Tu vas logiquement obtenir les mêmes relations à l'équilibre que par le théorème du moment statique mais les natures stables ou instables de ces équilibres sont plus faciles ainsi à déterminer.
Bonsoir,
Je vous remercie pour toute votre aide. J'ai essayé de rédiger une solution complète.
Comme vous avez dit l'énergie potentielle élastique est :
et l'énergie potentielle de pesanteur du cylindre est : pour la déterminer j'ai procédé de cette façon : on a besoin de la coordonnée suivant y de G , donc il suffit de faire le produit scalaire :
. En fait j'ai considérer la position de G à l'équilibre ( quand
, je ne sais pas si j'en ai le droit mais je pense puisque on cherchera les conditions d'équilibre , alors quand on fera
on prendra forcément
puisqu'on est en équilibre.
On a :
On note une position d'équilibre et on pose :
on trouve en faisant un développement limité au premier ordre et en éliminant deux termes :
On redérive pour déterminer le signe, on a : position d'équilibre stable.
D'où si la seule position d'équilibre est
 =0 et c'est une position d'équilibre stable.
=0 et c'est une position d'équilibre stable.
Vous avez dit précédemment que si alors le cylindre tombe de la demi-coquille, et si il tombait je ne pense pas qu'on aura ces conditions d'équilibres toujours valables puisqu'elles contiennent la masse du cylindre m , pour cela je suis allé voir la condition sur
quand
 >
> /2 , alors
/2 , alors .
Pour cela j'ai considérer que le cas : où
 =0 est une position d'équilibre instable et la deuxième position est stable puisque graphiquement on voit que la pente
=0 est une position d'équilibre instable et la deuxième position est stable puisque graphiquement on voit que la pente est plus grande que la pente de sin(
 ) en cette deuxième position. ( je ne sais pas si cela compte comme justification )
) en cette deuxième position. ( je ne sais pas si cela compte comme justification )
J'ai essayé de rédiger au mieux que je pouvais. J'espère que vous pourrez me rectifier les maladresses s'il y'en a.
Merci d'avance.
Il y a effectivement une difficulté dans le cas général lié au fait que ce problème possède deux degrés de libertés et
. L'étude dynamique ferait intervenir deux équations différentielles couplées. Mais, puisqu'on se limite aux situations d'équilibres, on peut je pense ce contenter de dire que, pour
donné, le minimum d'énergie potentielle du cylindre correspond à une altitude minimale de son centre de gravité, donc :
.
OK pour ton énergie potentielle :
Il suffit donc d'étudier le signe de la dérivée selon les valeurs de b en remplissant deux tableaux de variations comme cela se fait en math. Tu sais certainement faire cela !
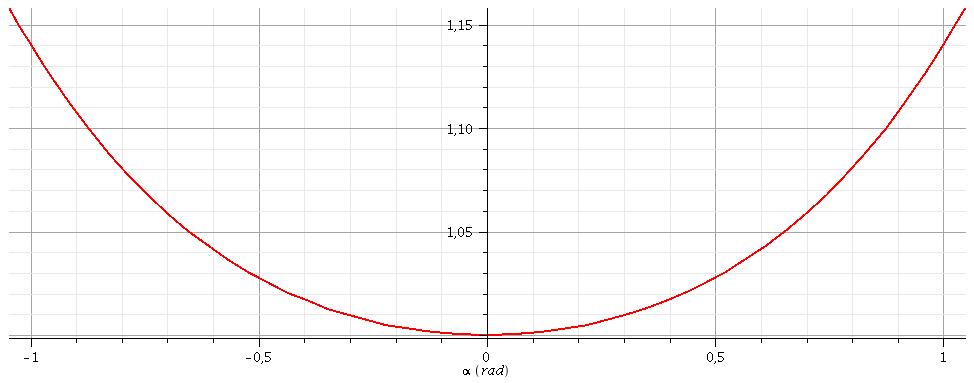
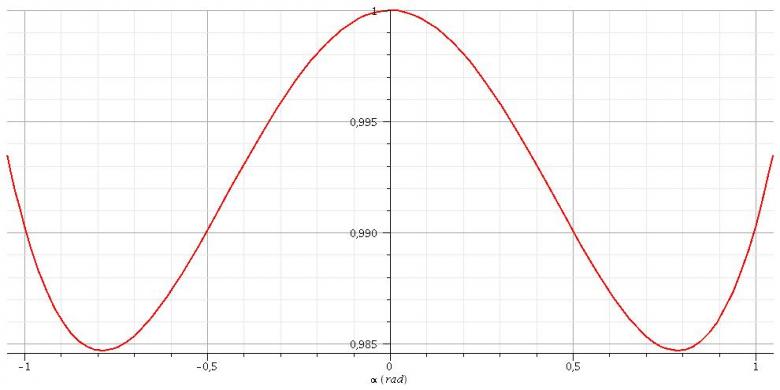
Pour illustrer cela et confirmer ce qui a été dit précédemment sur le nombre et la nature des équilibres, voici la représentation graphique des variations de Ep en fonction de pour deux valeurs de b différentes : b=1,2 puis en dessous : b=0,90. (échelle arbitraire pour l'axe vertical)
Bonjour,
Je vous remercie pour toute votre aide et votre patience. J'ai échoué à établir un tableau de variations pour le cas de b<1 à cause des deux autres solution differentes de 0. Pourtant je comprends bien grâce à votre schéma que dans le cas de b<1 les solutions differentes de 0 sont des positions d'équilibre stable.
Par contre en utilisant la propriéter de
 position d'équilibre stable. Car on remarque aux points d'intersection de la courbe y1=b et y2=sin(
position d'équilibre stable. Car on remarque aux points d'intersection de la courbe y1=b et y2=sin( )/
)/ la dérivée en ces points de y2 est inférieure à 0
la dérivée en ces points de y2 est inférieure à 0
Merci d'avance et je m'excude de vous importuner.
Je m'excuse pour le double post. Je rectifie ma réponse.
On travaille dans le cas de b<1.
pour
 =0 on a
=0 on a .
Mais on peut aussi voir : et pour

 0 :
0 : ce qui nous donne :
Pour  =
= 1>0 on a une pente négative de la fonction sin(
1>0 on a une pente négative de la fonction sin( )/
)/ , on trouve :
, on trouve :
Et pour  =
= 2<0 on a une pente positive de la fonction sin(
2<0 on a une pente positive de la fonction sin( )/
)/ mais
mais  2<0 d'où :
2<0 d'où :
Et de plus 0, 1 et
1 et  2 sont des positions d'équilibre, ce qui nous permet de conclure sur la stabilité.
2 sont des positions d'équilibre, ce qui nous permet de conclure sur la stabilité.
Vous en pensez-quoi s'il vous plait ? car j'ai essayé le tableau de variation mais seul le cas de b 1 que j'arrive à résoudre malheureusement.
1 que j'arrive à résoudre malheureusement.
Bonjour
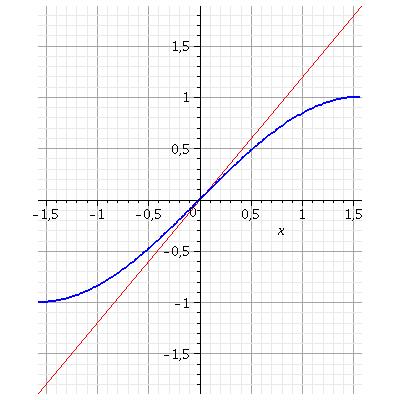
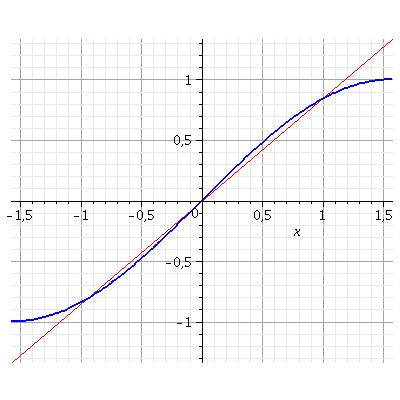
Pour étudier le signe de cette dérivée de Ep par rapport à  , on peut, dans un même repère, tracer la sinusoïde d'équation y1=sin(
, on peut, dans un même repère, tracer la sinusoïde d'équation y1=sin( ) et la droite d'équation y2=b.
) et la droite d'équation y2=b. . Ainsi, la dérivée de Ep par rapport à
. Ainsi, la dérivée de Ep par rapport à  a le signe de (y2-y1). Sachant que le coefficient directeur de la tangente en
a le signe de (y2-y1). Sachant que le coefficient directeur de la tangente en  =0 à la sinusoïde vaut (+1), on constate qu'il faut distinguer deux cas :
=0 à la sinusoïde vaut (+1), on constate qu'il faut distinguer deux cas :
b 1 et b<1. La position de la droite par rapport à la sinusoïde permet aisément de construire le tableau de variation dans les deux cas et d'arriver aux conclusions sur le nombre et la nature des équilibres.
1 et b<1. La position de la droite par rapport à la sinusoïde permet aisément de construire le tableau de variation dans les deux cas et d'arriver aux conclusions sur le nombre et la nature des équilibres.
Bonjour,
Je vous remercie pour votre aide. J'ai compris la démarche. Je suppose que dans un concours, ou dans un devoir surveillé où les calculatrices graphiques sont interdites.
Je vous remercie encore pour toute votre aide et votre effort.
Je m'excuse du double-post, par maladresse je n'ai pas terminé ma phrase : dans un concours, ou un devoir surveillé où les calculatrices graphiques sont interdites, ce genre de questions ne sera pas posé.
Je m'excuse du double-post, par maladresse je n'ai pas terminé ma phrase : dans un concours, ou un devoir surveillé où les calculatrices graphiques sont interdites, ce genre de questions ne sera pas posé.
Pourquoi pas ? Comme déjà expliqué, il suffit de savoir que la tangente à la sinusoïde en
 =0 vaut (+1) pour être capable de faire une étude qualitative. Evidemment, sans calculatrice sophistiquée, pas question de trouver les valeurs de
=0 vaut (+1) pour être capable de faire une étude qualitative. Evidemment, sans calculatrice sophistiquée, pas question de trouver les valeurs de  différentes de zéro correspondant à l'équilibre stable.
différentes de zéro correspondant à l'équilibre stable.

