Bonjour chocohoney,

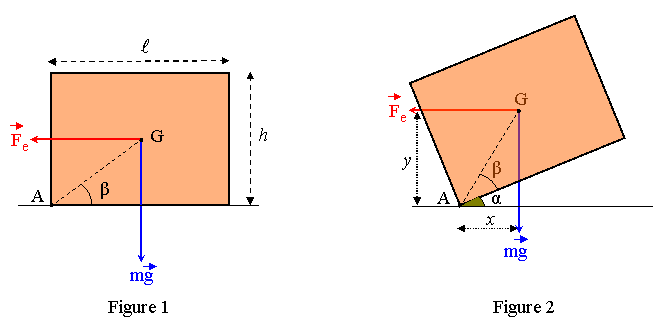
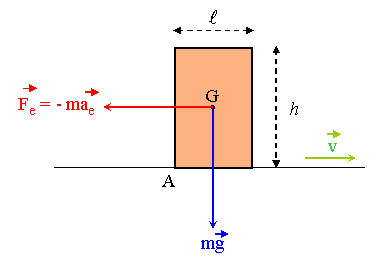
regarde la figure ci-dessous : j'appelle h = 2,5 m la hauteur du frigo et l = 1,0 m sa largeur ; le cote AB correspondant a sa profondeur est normal au plan de la figure. Le frigo ne glisse pas, donc le seul mouvement qui lui est permis est une rotation autour de AB. Cette rotation n'est possible que si la somme des moments par rapport a l'axe AB des forces appliquees en G tend a le faire tourner dans le sens direct (trigonometrique).
Deux forces sont appliquees en G :
1)  le poids mg du frigo, dont le moment prpt a A a pour norme M_p = mg.l/2, et qui tend a faire tourner le frigo dans le sens retrograde ;
2)  la force d'inertie d'entrainement F_e, dont la norme est m.a_e et dont le moment M_e par rapport a A est F_e.h/2. Le moment de F_e tend a faire tourner le frigo dans le sens direct.

Le frigo pivotera donc autour de AB si M_e M_p, soit a_e.h g.l, ou endore a_e (l/h).g = 0,4g.

Pour corser l'exercice, en supposant remplie la condition ci-dessus, saurais-tu ecrire l'equation differentielle qui donne l'angle (t) que fait le frigo avec l'horizontale ?  Reponse l'an prochain !

Prbebo.

Merci d'avoir pris le temps de me répondre en ce jour de fête.
Je n'aurais jamais pensé à mettre un axe normal au plan du dessin, et faire le calcul avec des moments de force !
Pour votre question :

somme des moments de forces = I    : accélération angulaire I:le moment d'inertie du frigo, considéré comme le quart d'un disque plein = mR² /4 = mh²/4 = Me + Mp
= -mah/2 + mgl/2
a=0,4g, il me semble que l'accélération linéaire est progressive, je ne sais pas comment l'exprimer en fonction du temps... à part que a=dv/dt...

et meilleurs voeux pour 2012 Prbebo !

Bonjour Chocohoney,

voici la réponse à la colle que je t'ai posée dans mon précédent message :

Voir figures 1 et 2 ci dessous : j'appelle l'angle constant que fait AG avec le fond du frigo, (t) l'angle que fait le fond du frigo avec la plate-forme horizontale du camion ((t) est la variable que l'on cherche), et (t) = (t) + l'angle entre AG et l'horizontale. La projection de AG sur l'horixontale et x = AG.cos, celle de AG sur la verticale est y = AG.sin.
Le théorème du moment cinétique conduit à J_A.d²dt² = F_ey - mgx, ou F_ey et mgx sont les moments des deux forces appliquées par rapport à l'axe de rotation AB, d²dt² l'accélération angulaire du bloc et J_A le moment d'inertie du frigo par rapport à l'axe AB.

Ecriture des moments :
La figure 2 montre que x = AG.cos = AG.(cos.cos - sin.sin). Avec AG.cos = l/2 et AG.sin = h/2 (cf figure 1), on arrive à x = (l/2)cos - (h/2)sin.
Un raisonnement analogue permet de trouver y = (l/2)sin + (h/2)cos.
La somme des moments des forces appliquées au frigo est donc m.sin.(la_e + hg)/2 + m.cos.(ha_e - lg)/2 = A.sin + B.cos.

Moment d'inertie par rapport à l'axe AB :
Il faut d'abord écrire le moment d'inertie J_G du bloc par rapport à l'axe de rotation // à AB mais passant par G, puis appliquer le théorème de Huygens :
J_G = m(h² + l²)/12 ;
md² = m.AG² = m.(h² + l²)/4.
On arrive à J_A = m.(h² + l²)/3.

L'équation différentielle du mouvement est donc de la forme C.d²dt² = A.sin + B.cos, A, B et C étant des constantes reliées aux données du problème (et dans lesquelles on peut simplifier par m).
Inutile de chercher une solution analytique, je crois qu'il n'y en a pas (pour mémoire, l'équation du pendule simple d²/dt² = -(g/l).sin, pourtant plus simple, n'a pas de solution). On peut juste remarquer que lorsque augmente à partir de 0, x diminue et y augmente, donc le moment du poids (celui qui maintient le frigo sur la plate-forme) s'efface devant celui de la force d'inertie, qui le tire vers l'arriere ; dès que l'angle dépasse /2, les deux moments sont de meme sens et donc additionnent leurs effets : autant dire que des que le frigo a commencé à se décoller de la plate-forme, il n'a plus aucune chance de revenir à la position horizontale.

Voila voila...  si tu as des questions n'hesite pas.

B.B.