Niveau école ingénieur

Équations d'équilibre-système de barres articulées

Posté par
souki 22-10-13 à 07:15

Bonjour tout le monde,

je dois trouver les équations d'équilibre dans le système de barres ci-dessous en utilisant deux méthodes. Je note R_A et R_C les réactions du support mobile sur A et C. Comme le déplacement de A (resp C) est nul selon x (resp y) alors R_A (resp R_C est porté par e_x (resp e_y).
La première méthode est l'application du principe fondamental de la statique.
Au noeud A, je trouve $R_A+N_{AC}\sqrt{2}{2}=0$ , et $N_{AB}+N_{AC}\sqrt{2}{2}=0$
Au noeud B, je trouve $N_{AB}=N_{BC}=0$
Et au noeud C : $F=N_{AC}\frac{\sqrt{2}}{2}+N_{BC}$ et $N_{AC}\frac{\sqrt{2}}{2}}=R_C$
SI on applique le PFD à toute la structure, on trouve aussi $R_C=0$ et $R_A+F=0$ , sauf erreur.
Ces équations sont suspectes, parce que leur résolution implique une force F nulle et des réactions aux supports nulles au niveau des points A et C (système hypostatique).

Une deuxième méthode est l'application du théorème des travaux virtuels. Ce dernier me donne seulement deux équations scalaires, à savoir : $N_{AB}+N_{AC}\frac{\sqrt{2}}{2}=0$ et $F=N_{AC}\frac{\sqrt{2}}{2}+N_{BC}$ .

Normalement, je devrais aboutir à un même résultat avec les deux méthodes. Donc il y'a forcément une erreur dans ce raisonnement. Merci de m'aider à l'exhiber.

Bien cordialement

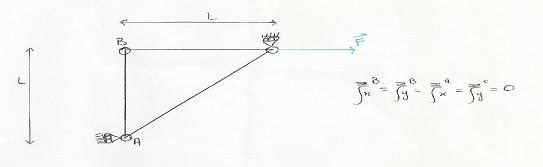
$Équations d\'équilibre-système de barres articulées$

Edit Coll : figure recadrée