Inscription / Connexion Nouveau Sujet
Équation polaire
Bonjour.
Voici l'énoncé de mon exercice.
On se place dans un référentiel R supposé galiléen auquel on associe le repère et on s'intéresse au système {point matériel M de masse m} soumis à une force
(a est une constante positive). À l'instant initial M est à la position M0 et
avec une vitesse
.
Questions :
a) Montrer que le mouvement de M est plan et déterminer le plan de la trajectoire.
b) Déterminer l'expression de l'énergie potentielle effective Ep,eff.
c) On considère maintenant que le système est dans un état de diffusion et on prend 
=
/2.
Établir que avec
et
.
Exprimer la conservation de l'énergie mécanique du système et en déduire l'équation différentielle : où
.
Déterminer l'équation polaire de la trajectoire avec les conditions initiales.
Donner l'allure de la trajectoire pour 
=0,1 ; 
0=0 ; r0=1 m.
Alors j'ai mis en bleu les seules questions qui me posent problème, mais j'ai préféré donner l'énoncé en entier par souci de clarté.
J'ai bien trouvé : puis finalement
.
Mais je n'ai aucune idée de l'allure de la trajectoire !
Je joins le fichier de correction avec le dessin de la trajectoire. Le problème, c'est que lorsque j'entre la formule de r() dans ma calculatrice, je n'ai pas du tout cela d'affiché.
Pouvez-vous m'expliquer comment on l'obtient ?
Merci par avance.
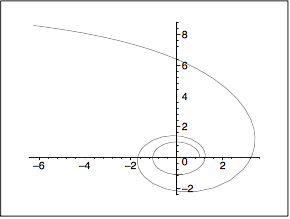
Voici ce que j'obtiens. J'ai un petit doute concernant la courbe que tu fournis : l'état t = 0 correspond à x=1m, y=0 avec une vitesse initiale suivant y. L'allure générale est la même.
Erreur possible : cette étude n'a de sens que pour
0
.</2
puisque la limite de r si (.) tend vers /2 est l'infini.
Soit, avec =0,1 :
0<5 rad
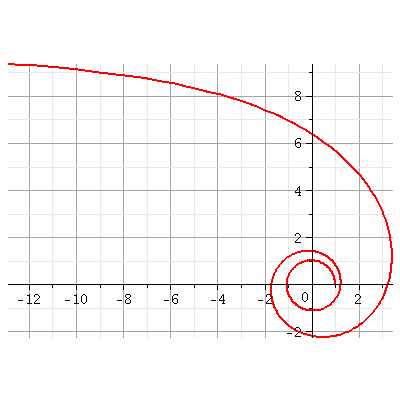
Personnellement, la courbe que je te poste correspond à compris entre 0 et 4,8 rad
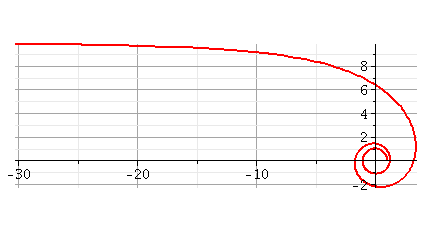
Je te poste aussi la courbe obtenue pour compris entre 0 et 4,9 rad
Je te laisse démontrer que, pour tendant vers (/2)rad, l'ordonnée y tend vers ro/...
Bonsoir et merci pour ta réponse.
Sur quel logiciel traces-tu tes courbes ? J'essaie désespérément sur calculatrice mais je n'obtiens pas d'écroulement, car ce n'est pas une vrai fonction au sens mathématique du terme, puisqu'un antécédent peut donner deux images !
Bonjour
Les courbes ont été tracées sous maple, logiciel de calcul formel. Je crois que les versions anciennes du logicielsont en téléchargement gratuit.
Si ta calculatrice graphique ne possède pas le mode "coordonnées polaires", il est peut-être possible de tracer la courbe en mode paramétrique . Ici :
x=r().cos() ; y=r().sin().
Bonjour.
Avec les coordonnées polaires, cela est déjà plus cohérent, en effet.
J'ai une Ti-83+ mais je n'ai pas la figure attendue.
J'ai rentré r=1/cos(0,1*) mais j'obtiens une espèce d'ellipse qui rebique vers la droite.
Comment exploite-t-on le fait que 0=0 ?
J'ai ressorti une vieille Ti... A priori, après s'être assuré d'être en mode radian et en mode polaire, le menu GRAPH possède un sous-menu RANGE où on peut rentrer i=0 puis f=4,8 (en rad).
Sur ma vieille machine, je n'arrive pas à voir la totalité de la courbe alors que tout fonctionne correctement en mode paramétrique (voir mon message du 16-04-17 à 10:48.
Annuler
connectez vous