Niveau master

Equation du mouvement d'un satellite terrestre

Posté par
ccopart 10-12-21 à 15:01

Bonjour,

Avec notre équipe, nous rencontrons un problème pour un projet d'école.

Nous avons besoin de récupérer la longitude et la latitude d'un satellite GPS en fonction du temps. Le but est de trouver une équation permettant d'avoir la latitude et la longitude du satellite pour tout t (en secondes minutes ou heure peu importe), c'est à dire ses coordonnées sphériques. L'altitude est quant à elle supposée constante, le satellite doit se situer en permanence à 20 000 km d'altitude de la Terre, qui elle est supposée parfaitement sphérique. L'équation de l'orbite doit donc décrire un cercle parfait, le mouvement est donc circulaire uniforme.

Nous avons déjà en notre possession la vitesse angulaire (qu'on suppose constante) ainsi que le rayon (20 000 km), et notre objectif sera de créer 6 orbites équitablement réparti comme vu sur le site suivant : http://subaru.univ-lemans.fr/AccesLibre/UM/Pedago/physique/02/divers/gps2.html
« Les satellites sont placés sur six orbites dont le plan est incliné de 55° par rapport au plan de l'équateur. Ces orbites sont décalées en longitude de 60° »

Cependant à partir de là, nous ne savons plus comment nous y prendre. Nous pensons avoir trouvé cette équation en 2D et en coordonnées cartésienne (https://fr.wikipedia.org/wiki/Mouvement_circulaire_uniforme)
x = r.cos(wt + θ)
y = r.sin(wt + θ)

Mais cela ne nous convient pas car nous l'aimerions en coordonnées sphériques (longitude-latitude pour le reste de notre projet).

Merci beaucoup si vous prenez le temps de nous aider,

Bien cordialement,

Charles.

Posté par re : Equation du mouvement d'un satellite terrestre 10-12-21 à 21:32

Bonsoir
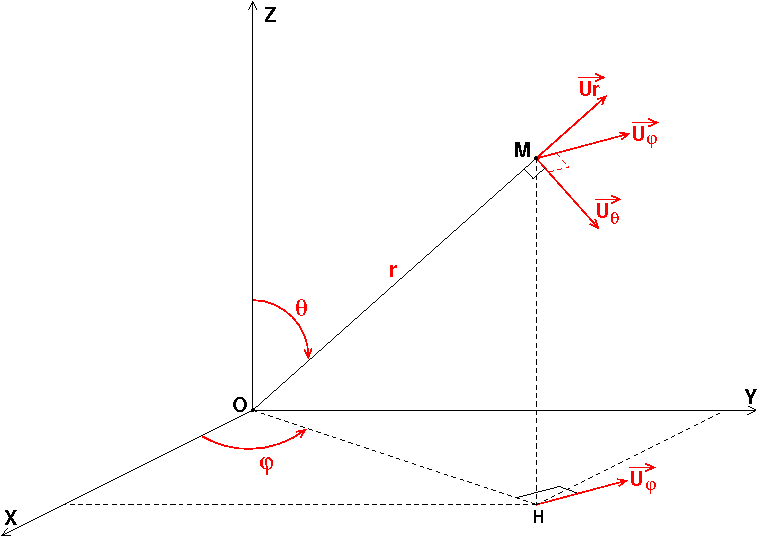
Petit schéma préliminaire pour bien préciser les coordonnées polaires. On note O le centre de la terre. Le repère cartésien dont tu parles pourrais être le repère $\left(O,\overrightarrow{u_{x}},\overrightarrow{u_{y}}\right)$ . Le repère géocentrique étant $\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)$ correspondant aux axes (Ox), (Oy), (Oz) de la figure. L'axe $\left(O,\overrightarrow{u_{x}}\right)$ correspond à l'axe vernal : il matérialise l'intersection du plan équatorial (O,x,y) avec le plan de la trajectoire de la trajectoire. Le vecteur $\overrightarrow{u_{x}}$ appartient donc au plan équatorial avec :

\varphi=\left(\overrightarrow{i},\overrightarrow{u_{x}}\right)

cet angle étant un multiple de 60°.

L'axe $\left(O,\overrightarrow{u_{y}}\right)$ est perpendiculaire à l'axe $\left(O,\overrightarrow{u_{x}}\right)$ mais incliné par rapport à l'axe (O,z) (l'axe des pôles) de l'angle . Ainsi :

$\overrightarrow{u_{x}}=\overrightarrow{i}.\cos\left(\varphi\right)+\overrightarrow{j}.\sin\left(\varphi\right)$

$\overrightarrow{u_{y}}=-\sin\left(\theta\right).\sin\left(\varphi\right).\overrightarrow{i}+\sin\left(\theta\right).\cos\left(\varphi\right).\overrightarrow{j}+\cos\left(\theta\right).\overrightarrow{k}$

Dans le repère $\left(O,\overrightarrow{u_{x}},\overrightarrow{u_{y}}\right)$ , la trajectoire est un cercle décrit à la vitesse angulaire . D'où le vecteur position du centre du satellite dans ce repère :

$\overrightarrow{OM}=r.\cos\left(\omega.t+b\right).\overrightarrow{u_{x}}+r.\sin\left(\omega.t+b\right).\overrightarrow{u_{y}}$

Reste à écrire ce vecteur dans le repère géocentrique $\left(O,\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\right)$ . Tu peux alors exprimer longitude et latitude en fonction des coordonnées précédentes mais cela ne va pas être très simple...

$Equation du mouvement d\'un satellite terrestre$