up

up

up

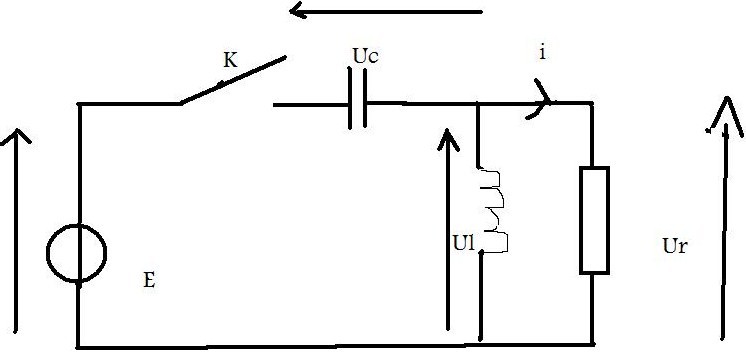
Je croyais que E=U?

Ensuite tu remplaces l'expression de chaque U par leurs formules respectives : U_R=RI, etc.

Et tu finis par tomber sur une équadiff avec I comme paramètre.

Au temps pour moi, j'ai mal regardé le schéma.

Mais avec les deux expressions de E que tu as, tu peux trouver deux équadiffs qui auront en commun une solution particulière.

Ah ok, je remplace et je te dis ensuite

Alors j'ai


Après j'ai pensé à dérivé pour faire apparaitre i grace au q et à multiplier par C

*dériver

Je pense que tu n'as pas besoin de ta dernière égalité, et en faisant la différence des deux premières tu obtiens ton équation finale, non?

Magnifique, merci pour le coup de main.
Par contre pour avoir l'allure de i(t), je dois résoudre cette équadiff. Equation caractéristique

on a ou
Donc

Je dois donc trouver les valeurs de A et B
A t=0, on i(0)=A+B=1 donc A=-B
Sur le schéma, est-ce que tu peux m'expliquer comment on trouve i(0+) et i(t) à une date de t>0?
Merci pour ton aide et ta patience

Salma, j'ai encore besoin de toi ^^

Alors là, désolée mais ce n'est plus de mon niveau!
Mais ça doit dépendre de la bobine?

Là aucune idée, je commence tout juste le chapitre, je vais continuer à chercher. En tout cas merci Salma
Si quelqu'un à une idéee pour trouver I(0+) et I(t) à t suffisamment long, qu'il se manifeste ^^.

De rien, désolée de ne pas pouvoir t'aider plus!