Inscription / Connexion Nouveau Sujet
Equation différentielle RC
Bonjour à tous,
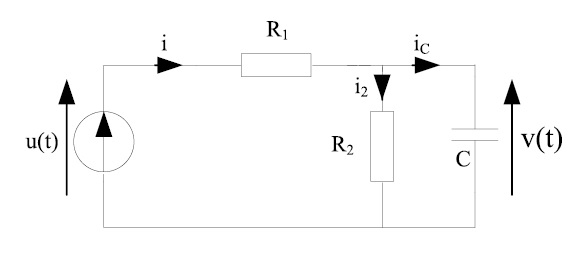
ci-joint le schéma du circuit qui me pose problème. On me demande d'écrire l'équation différentielle en v(t) permettant d'étudier ce circuit.
J'ai donc intuitivement répondu : dv/dt + 1/R1C v = U/R1C.
Cependant, d'après la correction, il faut prendre en compte R2. Or, on a exactement le même schéma en TD, et on nous demande de calculer l'évolution de v, et on ne prend pas en compte R2, car la tension au borne de R2 est égale à E. Enfin, je ne comprends pas vraiment quand es-ce qu'elle doit être prise en compte...?
Quelqu'un peut-il m'éclairer ?
Merci d'avance 
Bonjour bilou51
Tu as écrit que i=i2+ic
ic=C dv/dt
i2=v/R1
i=(u-v)/R2
Ton équation differentielle est donc: C dv/dt + (1/R1+1/R2)v = u/R2
Non?
*correction. Cependant, en TD, on nous a demander d'écrire l'equa diff pour voir l'evolution de v, et on a écrit :
V(t)=E(1-e(-t/R1C)).
Pourquoi, là, devrait-on prendre en compte R2 ? Et je ne vois pas vraiment comment vous arrivé à cette équation, i=(u-v)/R2, ah bon ?
En très développé :
u - R1.i - v = 0
i = i2 + ic
v = R2.i2
ic = C.dv/dt
-----
On élimine i :
u - R1.(i2 + ic) - v = 0
v = R2.i2
ic = C.dv/dt
---
On élimine i2 :
u - R1.(v/R2 + ic) - v = 0
ic = C.dv/dt
---
On élimine ic :
u - R1.(v/R2 + C.dv/dt) - v = 0
u -R1.C.dv/dt - v.R1/R2 - v = 0
R1.C.dv/dt + v.(1 + R1/R2) = u
dv/dt + v.(R1 + R2)/(R1.R2.C) = u/(R1.C)
-----
Sauf distraction. 
Oh, bah ça revient au même en fait  Surprenant !
Surprenant !
Mais pourquoi en TD on a pas fait ça ? Parce qu'on nous demandait l'equa diff pour l'évolution du condensateur et non pour étudier le circuit complet ?
Je vais essayer de repréciser ma question, car j'ai mal du formuler ma question, et je n'ai pas eu la réponse attendue, et vous m'en voyez fort perturbée ! 
J'ai deux exercices concernant ce circuit.
1er exercice : On me demander de calculer l'évolution de la tension du condensateur, et on obtient : v(t)=u(1-e(-t/R1C)).
2ème exercice : On me demande de donner l'équation différentielle en v(t) permettant d'étudier ce circuit. On obtient alors : dv/dt + ((R1+R2)/ (R1.R2.C)) * v(t) = u(t)/R1C.
Ma question est: pourquoi les réponses à ces deux questions sont différentes ? Pourquoi dans le premier cas on ignore totalement R2 tandis que dans le second on la prend en compte ?
Merci d'avance 
dv/dt + ((R1+R2)/ (R1.R2.C)) * v(t) = u(t)/(R1C) est l'équation différentielle qu'il faut résoudre pour en tirer v(t) = ...
Pour résoudre cette équation différentielle il est indispensable de connaître l'expression de u(t) ... qui n'est pas donnée ici.
... Et v(t) issu de la résolution de l'équation différentielle ne sera pas l'expression donnée en réponse à "1er exercice" quelle que soit l'expression non fournie ici de u(t).
Il y a donc visiblement une bisbrouille quelque part dans ce que tu écris.
Sauf distraction. 
On ne me demande pas une valeur, mais une expression représentant v(t), la tension aux bornes du générateur. Du moins, c'est ainsi que l'on a interprété cette question en résolvant cette exercice en TD.
v(t) = u (1-e(-t/R1C). (c'est l'expression générique de la tension aux bornes d'un condesateur que l'on voit en cours).
Je me demandais ceci : si on a pas les deux meme réponses à ces deux exercices, c'est parce que la première question correspond seulement au générateur, donc on ignore R2 ? Tandis que la deuxième question est plus générale et concerne le circuit entier, donc on prends en compte R2 ?
Pensez-vous que c'est pour cette raison?
De même, dans le schéma ci-joint, lorsque l'on a exprimer l'évolution du courant passant dans la bobine en fonction du temps, nous somme partis de E=Ur+UL. Donc nous avons totalement ignorer R.
Pourquoi? Je pense que c'est le même cas de figure
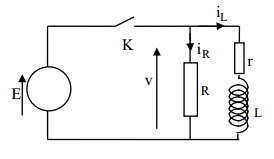
Dans ce dernier schéma, tu "ignores" R quend K est fermé car R et (r+L) sont "soumis" à E de manière presque indépendante.
Mais quand tu ouvres K, il n'y a plus que L, r et R (que tu n'ignores plus)
On est pas dans le meme cas que pour mon schéma de départ car la résistance r n'est pas placée au même endroit c'est ça?
"v(t) = u (1-e(-t/R1C). (c'est l'expression générique de la tension aux bornes d'un condesateur que l'on voit en cours)."
Il ne faut pas planter des formules qu'on n'a visiblement pas comprises.
Cette expression représente la tension à la charge d'un condensateur C à travers une résistance R1, l'ensemble étant alimenté par un générateur de tension u constante.
Elle n'est valable que si u est une constante et certainement pas quelle que soit l'expression de u(t).
Celle "formule" n'est pas valable non plus, même si u était une constante dans le schéma donné dans la question initiale.

Dans mon schéma de départ, on nous dit que :
On considère d'abord que u(t) évolue comme un échelon passant de 0 à U = 10V .
Mais, je ne comprends pas vraiment pourquoi cette formule ne convient pas dans mon premier schéma... Comment, et pourquoi, prendre en compte R2?
dv/dt + v.(R1 + R2)/(R1.R2.C) = u/(R1.C)
Avec u = E (constante), on obtient :
dv/dt + v.(R1 + R2)/(R1.R2.C) = E/(R1.C)
Qu'il faut résoudre.
-----
1°)
Solutions de dv/dt + v.(R1 + R2)/(R1.R2.C) = 0
v = K.e^-[(R1 + R2)/(R1.R2.C).t]
---
Solution particulière de dv/dt + v.(R1 + R2)/(R1.R2.C) = E/(R1.C)
v = E/(R1.C) * R1R2C/(R1+R2)
v = E . R2/(R1+R2)
---
Solution générale de dv/dt + v.(R1 + R2)/(R1.R2.C) = E/(R1.C) :
v = E . R2/(R1+R2) + K.e^-[(R1 + R2)/(R1.R2.C).t]
---
Avec la condition particulière v(0) = 0, on a :
0 = E . R2/(R1+R2) + K
K = - E . R2/(R1+R2)
Solution :
v(t) = E . R2/(R1+R2) - E . R2/(R1+R2).e^-[(R1 + R2)/(R1.R2.C).t]
v(t) = E . R2/(R1+R2) * (1 - e^-[(R1 + R2)/(R1.R2.C).t])
... qui n'est pas la même chose que v(t) = u (1-e(-t/R1C)).
-----
Si on fait tendre R2 vers l'infini dans l'expression v(t) = E . R2/(R1+R2) * (1 - e^-[(R1 + R2)/(R1.R2.C).t]) alors on retombe bien sur :
v(t) = E.(1-e(-t/(R1C))) ... ce qui est normal puisque faire tendre R2 vers l'infini revient à la supprimer du circuit et on retombe alors bien sur un simple circuit R1C alimenté par un générateur de tension continue E.
OK ?
-----
Il faut comprendre la "physique" d'un schéma et pas se référer à des analogies avec des circuits presque les mêmes ... mais pas tout à fait et qu'on ne maîtrise pas bien.
Tu écris :
"Comment, et pourquoi, prendre en compte R2?
Tu DOIS au moins t'apercevoir sans écrire la moindre formule que la valeur de R2 influence le résultat.
N'est-il pas évident par exemple que si R2 = 0 ohm (court-circuit), tu auras toujours v(t) = 0 V et certainement pas v(t) = E.(1-e(-t/(R1C))) ?
Et comment tenir compte de R2 ? ... Et bien comme je viens de le faire. En écrivant l'équation différentielle correcte et puis en la résolvant.
... ou bien (mais c'est pour plus tard quand on a un peu de pratique) on peut écrire la réponse finale sans calcul dans les cas simples (comme ici).
Sauf distraction.

Sauf distraction.



