Bonjour
Difficile d'être catégorique sans avoir de schéma et sans énoncé complet. Tout de même : tu peux obtenir une équation différentielle simple en dérivant par rapport à t l'expression obtenue puis en divisant tous les terme par car cette vitesse angulaire est non nulle au cours du mouvement.

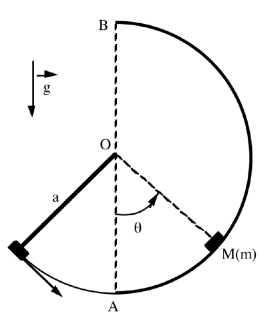
Un point matériel M de masse m est fixé à l'extrémité d'une tige OM de
longueur a, de masse négligeable, mobile sans frottement autour d'un axe
horizontal passant par O.
Soient OA et OB les positions d'équilibre stable et instable de OM.
1) La tige est abandonnée sans vitesse, M étant très légèrement à gauche de
B.
Quelle est la vitesse vA de M à son passage en A en fonction de g
(accélération de la pesanteur) et a ?
2) Au passage en A, M se détache de la tige et se met à glisser sans
frottement sur une demi - sphère de centre 0 et de rayon a.
a) Établir l'équation différentielle du mouvement de M sous la forme :
\dot{\theta }² =2\omega ²(1+cos\theta ) avec \omega ²=\frac{g}{a}

Voici l'énoncé complet avec l'équation qui est bien : avec

Merci pour l'énoncé. Mon message précédent concerne la simplification de l'équation différentielle. Sa démonstration utilise le théorème de l'énergie cinétique ou la conservation de l'énergie mécanique.

Oui en effet, j'avais réussi à démontrer l'expression l'équation différentielle, mais c'est vraiment au niveau de la résolution de cette dernière que je bloque. J'ai essayé de me ramener aux formules proposées mais je n'y arrive pas...

Si je comprends bien, tu as réussi à résoudre jusqu'à 2a. Quelles sont les questions suivantes  ?

C'est ça, voici les  dernières questions :
b) Résoudre cette équation différentielle pour obtenir la loi du
mouvement de M sur la sphère sous la forme : en précisant l'expression de .
On rappelle les formules suivantes :
et
3) Calculer la réaction R de la sphère en M en fonction de q.
Montrer qu'en un certain point C, M quitte la sphère. Calculer l'angle correspondant
, la vitesse de M en C et exprimer
numériquement en fonction de
  la durée T qui sépare les passages en A et en C.
4) Décrire brièvement le mouvement ultérieur de M

J'ai réussi, je pense, a exprimer R et j'ai trouvé : mg(3cos+2) et et v_C =

q = j'ai oublié de corrigé dans le message précédent

Sans énoncé complet... Mon premier message t'a orienté vers une mauvaise direction. Il faut plutôt prendre la racine carrée et séparer les variables :

(mettre un signe - en cas de mouvement dans le sens négatif)



Je te laisse intégrer en tenant compte des signes et des conditions initiales.

Très bien je vais essayer merci !