Inscription / Connexion Nouveau Sujet
équation différentielle
Bonjour, 
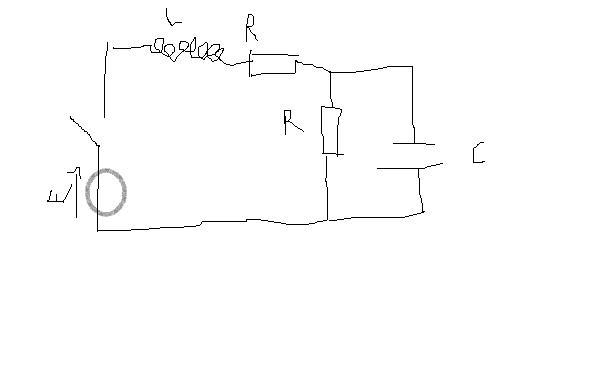
je bloque sur l'établissement d'une équation différentielle en i 
La forme de l'équation devrait être E/(RLC)= (d^2i/d^2t)+ 2y(di/dt)+ wo^*wo*i avec y et wo à déterminer pour le schéma que j'ai inséré à la fin de mon message
J'ai pensé d'abord trouver la résistance équivalente puisque les résistance sont en dérivations. Je trouve que Req= R/2 mais je ne suis pas sure que les deux conducteurs ont la même résistance cela n'est pas précisé mais étant donné que sur le schéma figure la même lettre R, j'ai considéré que c'était la même. Ensuite, je me suis ramené à un circuit RLC série soit
E= L* (d^2i/d^2t)+Req*(di/dt)+1/C*(i)
J'ai remplacé Req par R/2
E= L* (d^2i/d^2t)+(R/2)*(di/dt)+1/C*(i)
Mais voila on me demande d'établir l'équation sous la forme:
E/(RLC)= (d^2i/d^2t)+ 2y(di/dt)+ wo^*wo*i avec y et wo à déterminer.
Donc, j'ai transformé E= L* (d^2i/d^2t)+(R/2)*(di/dt)+1/C*(i)
J'ai abouti
E/RLC= (1/RC)*(d^2i/d^2t)+ 1/LC*(di/dt)+ 1/(C^2*R*L) ce qui ne va pas puisque je ne devrait pas avoir de coefficient devant la dérivée seconde

Z = pL + R + R/(1+pRC)
Z = (pL + 2R + p²LRC + pR²C)/(1+pRC)
Z = (p²LRC + p(L+R²C) + 2R)/(1+pRC)
E/i = Z
E/i = (p²LRC + p(L+R²C) + 2R)/(1+pRC)
LRC.d²t
d²i/dt² + (L+R²C).di/dt + 2R.i = E + RC dE/dt
LRC.d²i/dt² + (L+R²C).di/dt + 2R.i = E
d²i/dt² + [(L+R²C)/(LRC)].di/dt + (2/(LC)).i = E/(RLC)
-----
Reste à voir si on t'a enseigné cette méthode.
Sauf distraction, vérifie. 
Pardon, mais je ne vois pas à quoi correspond "Z" 
Hélàs on ne m'a jamais enseigné cette méthode.
Je pensais qu'en utilisant la loi des mailles ou des nœuds on pouvait s'en sortir mais je n'y arrive pas
Pas t'aiguillonner mais plutôt t'aiguiller.
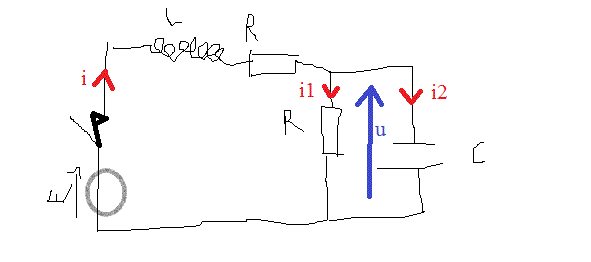
E - L di/dt - Ri - u = 0
u = E - L di/dt - Ri (1)
En dérivant (1), on obtient :
du/dt = -L.d²i/dt² - R.di/dt (2)
---
i = i1 + i2
i1 = u/R
i2 = C.du/dt
--> i = u/R + C.du/dt
Avec (1) et (2), on a alors :
i = (E - L di/dt - Ri)/R + C.(-L.d²i/dt² - R.di/dt)
i = E/R - (L/R) di/dt - i - LC d²i/dt² - RC di/dt
2i = E/R - ((L/R) + RC) di/dt - LC d²i/dt²
LC d²i/dt² + ((L/R) + RC) di/dt + 2i = E/R
d²i/dt² + ((L/R) + RC)/(LC) di/dt + 2i/(LC) = E/(RLC)
d²i/dt² + [(L + R²C)/(RLC)] di/dt + (2/(LC)).i = E/(RLC)
-----
Sauf distraction. 
merci beaucoup  J'ai tout compris
J'ai tout compris 
J'ai pu continué l'exercice; Pourriez-vous me dire si ce que j'ai fait est juste
1) Ainsi on devait trouver une équation de la forme
[b]E/(RLC)= (d^2i/d^2t)+ 2y(di/dt)+ wo^*wo*i[/b avec y et wo à déterminer
Donc avec d²i/dt² + [(L + R²C)/(RLC)] di/dt + (2/(LC)).i = E/(RLC), on trouve que
wo= ( 2)/
2)/ (LC)
(LC)
y= (L+R*R*C)/(2RCL)
Ensuite, on demande:
2) déterminer le facteur de qualité Q puis en posant RC=  et RC=L/R, donnez l'expression de wo, y et Q.
et RC=L/R, donnez l'expression de wo, y et Q.
On a Q= (L/R)* wo par définition donc Q= (L/R)* ( 2)/
2)/ (LC)
(LC)
Donc Q= *(
*( 2)/
2)/ (LC)
(LC)
Ensuite: wo= ( 2)/
2)/ (LC)
(LC)
Je ne pense pas que lon puisse transfomer son écriture en fonction de 

Puis y=(L+R*R*C)/(2RCL)
Donc y= 1/(2 )+
)+  /(2LC)
/(2LC)
3) On me demande alors combien faut-il de conditions initiales pour résoudre entièrement l'équation ? Donner la valeur de chacune des conditions initiales trouvées.
J'ai répondu qu'il fallait 2 conditions initiale: la valeur de i à t=o quand l'interrupteur et ouvert et di/dt à t=0
Soit i=0 à t=0 car interrrupteur ouvert et di/dt =0 par continuité du courant imposée par la bobine
4) Résoudre l'équation différentielle à la condition RC=L/R
Soit on a y= 1/(2 )+
)+  /(2LC) avec
/(2LC) avec  =RC
=RC
donc 2y=1/( )+
)+  /(LC)
/(LC)
wo*wo= 2/LC;
On sait que l'équation est de type :
[b]E/(RLC)= (d^2i/d^2t)+ 2y(di/dt)+ wo^*wo*i[/b
Donc on remplace
on trouve:E/(RLC)= (d^2i/d^2t)+ [1/( )+
)+  /(LC)](di/dt)+ (2/LC)*i.
/(LC)](di/dt)+ (2/LC)*i.
Je n'ai plus qu'à résoudre cette équation comme en maths n'est-ce pas et à faire des disjonctions de cas avec discriminant positif ou négatif ou nul ? 
J'ai à nouveau un problème en ce qui concerne discriminant du polynôme caractéristique associé à l'équation homogène.
L'équation homogène est
X^2+ [1/( )+ /(LC)] X+ (2/LC)=0
)+ /(LC)] X+ (2/LC)=0
je calcule le discriminant et je trouve:
d= (LC+ ^2-8
^2-8 )/ (
)/ ( *LC)
*LC)
le signe du discrimant va donc dépendre du numérateur
On sait que  =RC
=RC
On peut transformer l'écriture du numérateur:
on trouve (LC+ ^2-8
^2-8 )= (LC+(RC)^2-8RC)
)= (LC+(RC)^2-8RC)
Or RC=L/R donc (LC+(RC)^2-8RC)= L(C+(L/R^2)-8/R)
Et voila je me posais la question de savoir si je ne devais pas considérer le discriminant toujours négatif pour me placer dans un régime pseudo-périodique ?
D'autant plus que la question suivante est de tracer l'allure de i (sous-entendu il n'y en qu'une seule) alors que si je fais une disjonction de cas j'aurais 3 courbes
Je n'ai pas vérifié tout ce que tu as écrit.
J'ai cependant repéré une erreur pour une des conditions initiales.
(di/dt)(0) = E/L et pas 0 comme tu l'as écrit.
En effet, en t = 0, La tension sur L est E et pas 0 et don ...
-----
Je n'ai rien regardé avec le Q et le wo et j'ai traité directement le cas de RC = L/R sans introduire Q et wo et tau (mais tu devrais toi le faire puisque c'est demandé).
Avec RC=L/R, l'équation d²i/dt² + [(L + R²C)/(RLC)] di/dt + (2/(LC)).i = E/(RLC) devient :
d²i/dt² + (2/(RC)) di/dt + (2/(R²C²)) i = E/(R³C²)
p = -1/(RC) +/- V[(1/(R²C²) - 2/(R²C²)]
i(t) = e^(-t/(RC).(A.cos(t/(RC)) + B.sin(t/(RC)) + E/(2R)
i(0) = 0 --> A = -E/(2R)
(di/dt)(0) = E/L
-A/(RC) + B/(RC) = E/(R²C)
-A + B = E/R
B = E/R -E/(2R)
B = E/(2R)
i(t) = [E/(2R)] * [1 - e^(-t/(RC).(cos(t/(RC)) - sin(t/RC))]
C'est cette courbe dont il faut dessiner l'allure...
Pas de question donc à se poser sur le discriminant...
-----
Je n'ai rien vérifié. 
J'ai à nouveau un problème j'ai oublié de prendre en compte que le condensateur est initialement déchargé donc je ne sais pas is cela change quelque chose mais il me semble que oui parce que à ce moment i2 initialement établie vaut 0  non ?
non ?


