Niveau licence

équation de continuité (dynamique des fluides)

Posté par
ferenc 08-10-13 à 12:58

Bonjour, on me dit dans un énoncé:
Soit $V$ un volume fixe (c'est donc une description eulérienne).
Je ne comprend pas pourquoi ça ne pourrait pas être une description lagrangienne ?
merci

Posté par re : équation de continuité (dynamique des fluides) 08-10-13 à 12:59

* Soit un volume $V$ fixe $\text{\red dans un fluide}$ .

Posté par Equation de continuité 2 08-10-13 à 14:08

Bonjour, je ne comprend pas la démonstration suivante.
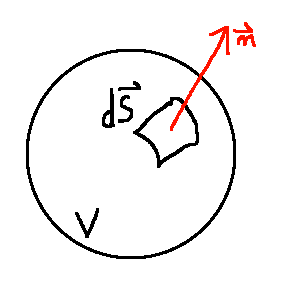
Soit $V$ un volume fixe dans le fluide. Nous supposons qu'il n'y a pas de réaction nucléaire qui change la masse du fluide.
La variation de la masse due à la variation de la densité est donc égale au flux de masse $\rho\bold u$ à travers la surface $S$ entourant le volume $V$ ;

Q1) Pourquoi le flux de masse vaut $\rho\bold u$ ?

La variation de la masse incluse dans $V$ est $M(t)=\int_V d^3\rho(\bold r, t)$

Q2) Je ne comprend pas d'où vient cette formule. Dieu peut-être ?

Ainsi, $\frac{d M(t)}{dt}=\frac{d}{dt}\int_V d^3r\rho(\bold r,t)=\int_V d^3r\frac{\partial \rho(\bold r,t)}{\partial t}$ .

Q3) Pour moi, $\frac{d\rho(\bold r,t)}{dt}=\frac{\partial \rho}{\partial t}+(\bold u\cdot\nabla)\rho$ , pourquoi aurions nous que $(\bold u\cdot \nabla)\rho=0$ ? Serait-ce dû au fait que dans une description eulérienne, $\bold r=cste$ ? (je n'en suis d'ailleurs même pas sûr que $\bold r=cste$ dans une description eulerienne).

Le changement de masse $\frac{dM(t)}{dt}$ est égale au flux de masse $\rho\bold u$ à travers la surface, d'où:
$\frac{dM(t)}{dt}=-\int_S d^2 r\rho \bold u\cdot\bold n=-\int_S d\bold S\cdot (\rho\bold u)$

La normale $\bold n$ étant dirigé vers l'extérieur, le signe $-$ se conçoit aisément. En effet pour que $\frac{dM}{dt}$ soit positif, il faut qu'il y ait un flux de masse qui rentre dans $V$ : si $\bold n$ est dirigé vers l'extérieur de $V$ , le flux de masse $\rho\bold u\cdot \bold n$ est alors négatif, d'où le signe moins. La dernière égalité et le théorème de la divergence nous permette de conclure.

Q4) Je ne comprend pas pourquoi $\frac{dM}{dt}$ doit être positif ni pourquoi le flux de masse vaut $\rho\bold u\cdot\bold n$ et non pas $\rho\bold u$ comme on a pu le stipuler précédemment.

Merci pour vos réponses

Equation de continuité 2

*** message déplacé ***

Posté par re : Equation de continuité 2 08-10-13 à 14:09

errata:
La variation de la masse incluse dans $V$ est $M(t)=\int_V d^3{\red r}\rho(\bold r, t)$

*** message déplacé ***

Posté par re : équation de continuité (dynamique des fluides) 08-10-13 à 14:26

@moderateur: ce n'est pas entièrement la même question

@celui_qui_va_me_répondre: Pour Q1) ne devrions nous pas tout simplement avoir $M(\bold r, t)=\rho(\bold r, t)$ ? Je n'arrive pas à faire le parallèle avec l'intégrale.

merci

Posté par re : équation de continuité (dynamique des fluides) 08-10-13 à 14:27

PS: on va appeler la question de mon premier post (à savoir de 12:58) Q0)

Posté par re : équation de continuité (dynamique des fluides) 16-10-13 à 20:48

Bonjour,

On fait un bilan de masse ou de n'importe quoi toujours de la même façon :

ce qu'il y a dans le volume V à l'instant t+dt = ce qu'il y avait à t + ce qui est entré - ce qui est sorti.

Comme je n'ai pas le temps de détailler et que ça peut être assez long, je préfère vous renvoyer vers ce cours : paragraphe "Mécanique des Milieux Déformables (PH314)".

La conservation de la masse est traité au chapitre "Dynamique", mais utilise un formule importante démontrée au chapitre "Cinématique" ainsi que dans les chapitres précédents.

Pour une démonstration plus proche de "ce qu'il y a dans le volume V à l'instant t+dt = ce qu'il y avait à t + ce qui est entré - ce qui est sorti" il y a ce cours notamment en mécanique, le chapitre 4 "Description d'un fluide".

D'ailleurs, commencez peut-être par lire la 2nde référence...

Posté par re : équation de continuité (dynamique des fluides) 16-10-13 à 20:52

merci infiniment alba,
je vais étudier tout ça avec attention et vous ferez un retour si nécessaire

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de physique - chimie

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

équation de continuité (dynamique des fluides)

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique