equation d'etat a partir des coefficients thermoelastiques : exercice de sciences physiques de maths sup

 Niveau maths supPartager :
			        
equation d'etat a partir des coefficients thermoelastiques
Posté par 
yosh2  24-04-21 à 19:56
bonjour

pourriez vous m'aider a déterminer l' équation d'etat d'un fluide a partir des coefficients thermoélastiques , pour un fluide avec =1/T et =1/T,

ne connaissant pas la démarche pour traiter de tel exo , j'ai fait quelque recherche sur internet et j'ai cru comprendre que je devais utiliser la différentielle , je dispose de 3 variables P, T et V j'ai donc fait 

dP = (dP/dV)dV + (dP/dT)dT puis a partir de = 1/V(dV/dT) et  = 1/P(dP/dT) je trouve dP = (P/V)dV+(P/T)dT et la je ne sais pas quoi faire ensuite.

merci
 Posté par 
vanoisere : equation d'etat a partir des coefficients thermoelastiques  24-04-21 à 20:49
Bonsoir

En posant P=f(V,T) avec f a priori inconnue, la différentielle de P a pour expression générale :

En identifiant puis en intégrant...
 Posté par 
vanoisere : equation d'etat a partir des coefficients thermoelastiques  24-04-21 à 21:26
J'ai posté mon premier message sans vérifier ton expression de la différentielle de P.

Réfléchis au réalisme de ton résultat : augmenter la pression à température fixe entraîne une diminution de volume donc nécessairement :

Peux-tu expliquer rigoureusement comment tu as obtenu l'expression de la différentielle dP ?
 Posté par 
yosh2re : equation d'etat a partir des coefficients thermoelastiques  24-04-21 à 23:09
bonsoir

en partant de 

j'ai remplace  par P/T en utilisant =1/P(dP/dT)=1/T 

et ensuite j'ai fait  (en effet j'avais oublie le -)au final 

 Posté par 
vanoisere : equation d'etat a partir des coefficients thermoelastiques  24-04-21 à 23:18
Nous sommes d'accord maintenant ! Tu peux donc utiliser la méthode proposée dans mon message du  24-04-21 à 20:49.
 Posté par 
yosh2re : equation d'etat a partir des coefficients thermoelastiques  24-04-21 à 23:38
bonsoir

en identifiant on trouve  puis  en integrant entre P et P0 , V et V0

j'obtiens ln(P/P0) = -ln(V/V0) ensuite PV=P0V0 et puis de meme avec l'autre terme on trouve PT0 = P0T , est ce correct ? que faire à présent?

merci
 Posté par 
vanoisere : equation d'etat a partir des coefficients thermoelastiques  25-04-21 à 12:43
Bien vu pour le passage aux logarithmes. De :

On tire, comme tu l'as fait : P.V=constante à T constante. Donc, de façon générale : P.V=f(T) où f est une fonction à déterminer à partir du second terme de la différentielle :

 et, puisque :    :  

Par identification :

 ; soit :

Facile de vérifier que cette équation différentielle admet comme solution : f(T)=K.T où K est une constante. Conclusion : l'équation d'état est :

On retrouve l'équation d'état d'un gaz parfait avec K=n.R.
 Posté par 
yosh2re : equation d'etat a partir des coefficients thermoelastiques  25-04-21 à 13:56
bonjour

j'ai essaye de refaire la meme demarche pour =R/(RT+bP) et 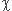 = RT/P(RT+bP)  , je trouve 

 en identifiant  on trouve P/T = f(V) puis 

donc  cad 

l'equa diff n'étant pas linéaire je ne sais pas comment la resoudre j'ai donc utiliser un outil sur internet qui me donne f(V) = 1/(V(b/Rlog(V)+cte)) donc P=T/(V(b/Rlog(V)+cte)) 

mais le log me laisse un peu perplexe .pourriez vous vérifier mon travail ?

merci 
  Posté par 
vanoisere : equation d'etat a partir des coefficients thermoelastiques  25-04-21 à 14:54
Tu trouves l'énoncé ici, page 3, paragraphe III.C) accompagné d'un peu d'aide sur la résolution.

Le corrigé est fourni page 8 et 9.