Inscription / Connexion Nouveau Sujet
Equation Cinétique
Bonjour,
Je me rends compte aujourd'hui que j'ai du certainement louper certaines bases de la cinétique.
Dans le système bielle-manivelle dessiné sur l'image joint, je cherche à retrouver par moi même l'équation de la position du point B (noté Xb), mais aucun moyen d'y parvenir...
La 2ème image montre le raisonnement que j'ai fais, je ne comprends toujours pas quelle est mon erreur...
Besoin d'aide pour m'explique quelle est mon erreur svp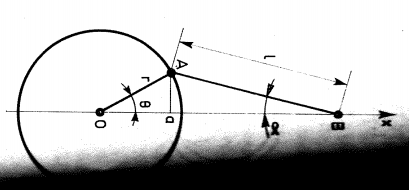
* mmalou > Image recadrée, sur la figure uniquement ! Si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé ainsi que tes recherches sur le forum  *
*
Bonsoir
Attention : les énoncé très court comme celui-ci doivent être copiés. Seul le schéma doit être scanné.
Essaie aussi d'écrire les formules plutôt que de les scanner.
Sinon : ta projection du vecteur AB sur l'axe horizontal est fausse.
Bonjour,
C'est correct à une erreur de signe près : , par lecture du dessin.
Je ne comprends pas par ailleurs d'où sort la composante sur x de , on a l'impression que vous utilisez votre résultat.
Je retiendrai la gestion des posts la prochaine fois alors.
Pourquoi fausse ? je n'arrive pas à comprendre. Merci de me donner plus d'explications si possible
Attention aussi : l'origine des abscisses du point B n'est pas le point O du schéma... Ce qui est un peu piégeant !
C'est donc la projection suivant x du vecteur AB qui me fait defaut.
Pouvez vous me faire une petite demonstration ?
Le point A n'étant pas situé à l'origine O m'embrouille le raisonnement...
Avec tous ces posts croisés, on finit par ne plus rien comprendre ! J'ai répondu oui concernant la distance OB = r.cos( )+l.cos(
)+l.cos( )
)
Ton message de 19h09 est évidemment faux : in vecteur ne peut être égal à un réel et r doit intervenir !
désolé pour le croisement de message.
Si xB = r.cos + l.cos
+ l.cos , d'où sort alors le l + r present dans l'énoncé ?
, d'où sort alors le l + r present dans l'énoncé ?
la formule de l'énoncé est fausse ??
Le texte du problème ne semble pas préciser d'origine des abscisses. Dans ce cas, le plus simple, à mon avis est de s'en remettre au schéma et de considérer le point O comme origine. Pourquoi ce corrigé cherche-t-il ainsi à compliquer la situation ?


