Inscription / Connexion Nouveau Sujet
Équation aux dimensions - Bombe atomique 16/07/45
Bonsoir.
Je fais un exercice sur les équations aux dimensions et j'observe un résultat incohérent avec la réalité.
Je pense donc qu'il y a une faute quelque part que je n'arrive pas à la déceler.
données :
- tel que
est une constante qu'on ne cherche pas à déterminer
- km/s
- kg/m3
- J
-valeurs de surpressions : kPa (constructions détruites),
kPa (destruction des murs non renforcés),
kPa (personne renversée par l'onde de choc),
kPa (bris de vitre).
On me demande de calculer : la distance à laquelle on doit se trouver de la bombe pour être en sécurité
j'ai donc l'équation aux dimensions suivantes :
à laquelle j'associe le système :
(je vous laisse le vérifier si vous ne me croyez pas parce que j'avoue qu'il y a plus passionnant que d'écrire des systèmes en latex
 )
)
J'ai donc identifier mes exposants pour répondre à la question j'ai besoin du rayon de l'onde de choc ("sphère") et je connais la vitesse de propagation de l'onde.
Il vient :
Voilà mon soucis : En faisant l'application numérique je trouve des valeurs de rayons de l'ordre de km pour être en sécurité de bris de glace et presque
km pour ne pas être renversé par l'onde de choc. Ces valeurs sont-elles cohérentes.
Je joins à cela un tableur avec toutes les données.
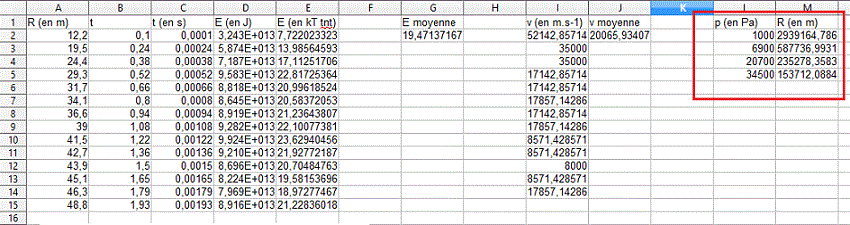
Bonsoir
tel que K est une constante qu'on ne cherche pas à déterminer
L'énoncé précise-t-il que K est sans dimension ?
les distances que tu obtiens me paraissent beaucoup trop élevées. Il s'agit tout de même de la première explosion nucléaire de l'histoire...
c'est tout à fait ce que je pense aussi.
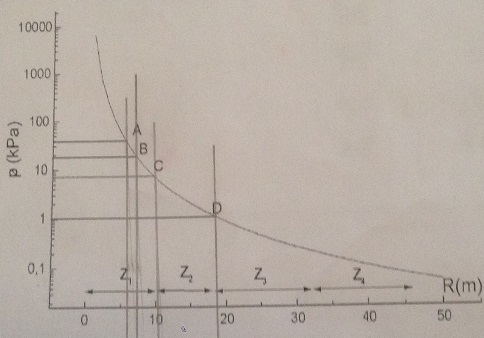
d'autant qu'après dans la suite des questions j'ai une courbe qui représente la surpression en fonction du rayon de l'onde de choc (bon OK, je dois en faire un commentaire/critique, mais je ne pense pas que la différence soit si grande) ici on a mètres pour la limite du bris de glace, dans mes calculs on a
kilomètres, soit un petit facteur
entre les deux mais tout va bien

Je viens de vérifier tes calculs conduisant à l'expression de R. J'obtiens la même chose que toi. N'ayant ni la valeur de K ni celle de v, je ne peux vérifier la suite.
je n'ai pas la valeur de non plus, celle de
étant déterminé à partir des images que suit (il faut mesurer à la règle les champignons puis convertir, choses faites dans mon tableur)
source: https://questions2physique.wordpress.com/2012/03/10/un-secret-nucleaire-mal-garde/

Je ne comprend pas comment le rayon de la "sphère" noté
peut ne pas être égale au produit de la vitesse de la sphère noté par le temps
qu'elle a mis à parcourir cette distance
l'expansion n'est pas uniforme, v dépend du temps
mais ce n'est pas un problème
on a R=R(t) grâce aux clichés, donc en inversant t=t(R) et p = p(R)
pour t = 0.24 ms, R = 19.5m et on devrait trouver p=1000 Pa d'après la courbe
mais comme K est inconnu...
et qu'il est tard 
Le fait que l'expansion ne soit pas uniforme c'est une chose,
je pensais l'avoir rétabli en prenant la moyenne de toutes les vitesses "instantanées"
mais c'est vrai que calculer des vitesses comme ceci ça fait un peu collégien :/
je n'ai pas du tout tenu compte des infos sur le site que j'ai associé à l'un de mes messages, je le découvre comme vous et ce je t'avoue que je ne saurais pas le redémontrer
Rappelons que je connais la valeur de et
à une constante près.
et
(ce sont ces formules là, objets de questions précédentes, qui m'ont permis de faire le tableur.)
j'ai donc pensé que si je remplaçais dans
je pourrais isoler mon R et trouver une relation avec les autres paramètres.
Chose faite :
Mais là encore nouveau problème je ne sais pas quelle valeur de utiliser
bonjour,
c'est difficile de t'aider car on ne connait que des bribes d'énoncé et on ignore les questions et surtout l'ordre des questions
je tente ma chance malgré tout:
tu as trouvé une relation empirique plausible p = p(E,rho,t)
pour la valider il faut des données expérimentales (rien ne dit que p dépend bien de ces paramètres-là)
et ici, le mieux, c'est une courbe log/log
on a: 5log p = log K + 3log rho + 2log E -6log(t)
donc pour une explosion donnée (E et rho donnés) 5 log p = A - 6log t A étant une cste
on trace Y = f(X) avec Y = 5log p et X = log(t) et on doit trouver une droite (il faut évidemment des données expérimentales (p,t), au moins qqes points)
une fois que tu as Y=f(X) tu peux répondre à tes questions puisque tu as R=R(t) d'un côté (clichés) et log p = f(log t) en extrapolant
Je reprend plus clairement alors :
Les seuls données que j'ai son celle de la photo associé au post du 10-09-15 à 21:13 (de là j'ai mesuré les rayons à la règle puis converti grâce à l'échelle en bas d'image, j'ai aussi les données de temps) Voilà comment les 3 premières colonne de mon tableur se construisent.
la première question est :
1-Établir la loi d'évolution temporelle du rayon de l'onde de choc (par une équation aux dimensions) sachant qu'il y a une dépendance de la masse volumique de l'air non perturbé
j'ai trouvé la réponse à cette question
2- En déduire une estimation (voilà pourquoi la constante n'a pas besoin d'être connue) de l'énergie libérée
j'ai répondu à cette question (voir tableur) et ma valeur est très proche de celle communiquer dans le sujet (18 kt TNT)
3- les dégâts causés par une explosion dépendent localement de la surpression
(c'est là que j'ai mes 4 valeurs de surpression)
déterminer les exposants dans tel que
est une constante adimensionnée
LA QUESTION 4 celle que je cherche depuis le début
calculer la distance à laquelle on doit se trouver de la bombe pour être en sécurité
5- commentez la courbe associée au post du 10-09-15 à 19:55
voici tous les éléments dans l'ordre j'espère que ça aidera
la 1 et la 2 correspondent à la formule trouvée par Taylor
R5  (E/
(E/ ) t2
) t2
et comme K 1 on arrive à trouver E avec les données fournies
1 on arrive à trouver E avec les données fournies
3) on a: p5
 3 E2 /t6
3 E2 /t6
donc en combinant 1) et 3) on a: p E/R3
mais on ignore le coeff. de proportionnalité
on sait juste que p R3 est une cste
4) je ne vois pas (avec les éléments que tu as donnés)
5) cette courbe ne correspond pas à une explosion de 18kt
d'après le Web on a p=7kPa à plus de 5km
mais p R3 = cste pourrait être vérifiée
merci quand meme pour le temps passé et l'aide
je vais essayer de m'en sortir avec tous les éléments qu'on a donné

 vt car d'après le Web, R(t)
vt car d'après le Web, R(t) 

