Inscription / Connexion Nouveau Sujet
Equa diff rlc
Bonjour,
je suis totalement bloquée dans l'établissement de mon équadiff en Il (courant traversant la bobine). 7
J'ai U=Ul+UR1 = L diL/dt + Uc + R2C dUc/dt... Mais je dois passer de Uc, à des courants. Où alors il faut exprimer autrement UR1, mais je ne vois pas comment.
Quelqu'un peut-il m'aider ? 
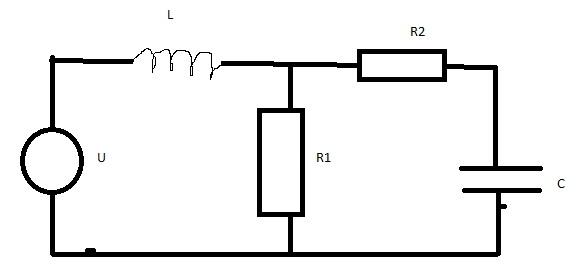
Même problème en fonction de Uc :
U= UL+UR1
= LdiL/dt + Uc + R2
=L d(iC+iR)/dt + Uc + R2iC
=LC d²Uc/dt² + LdiR/dt + Uc + R2C dUc/dt
(avec iL le courant dansla bobine, iC le courant dans le condensateur et R2) et iR le courant dans R1)
Salut,
Personnellement je fais ça en complexe
U=Zeq totale* i
Détermonation de Zeq
R2 + 1/(jCw)=(jCR2w + 1)/(jCw)
Zeq de R1//((jCR2w + 1)/(jCw))
=R1*((jCR2w + 1)/(jCw))/(R1+(jCR2w + 1)/(jCw))
=R1*(jCR2w + 1)/(jCR1w+jCR2w + 1)
Zeq totale = jLw + R1*(jCR2w + 1)/(jC(R1+R2)w + 1)
Je ne suis pas trop à l'aise avec cette méthode, mais je propose:
U=Ul+UR1
= L diL/dt + Uc + R2*i2
= L diL/dt + 1/C * i2 + R2*i2
i2 + R2*i2
or
iL=i1+i2
et
1/C * i2 + R2*i2 = R1*i1
i2 + R2*i2 = R1*i1
1/C * i2 + R2*i2 = R1*(iL-i2)
i2 + R2*i2 = R1*(iL-i2)
R1*iL = 1/C * i2 + (R2+R1)*i2
i2 + (R2+R1)*i2
iL= = 1/(R1*C) * i2 + (R2+R1)*i2/R1
i2 + (R2+R1)*i2/R1
donc
U=L diL/dt + 1/C * i2 + R2*i2
i2 + R2*i2
=L*d(1/(R1*C) * i2 + (R2+R1)*i2/R1) + 1/C *
i2 + (R2+R1)*i2/R1) + 1/C * i2 + R2*i2
i2 + R2*i2
= 1/C * i2+ L/(R1*C)*i2 + R2*i2 + L(R1+R2)/R1*di2/dt
i2+ L/(R1*C)*i2 + R2*i2 + L(R1+R2)/R1*di2/dt
en espérant n epas mettre trompé
Oulaa ! On peut avoir une primitive dans une équa diff? Dans ce genrede circuit (avec condensateur+bobine), il n'est pas possible d'obtenir un équation différentielle aussi simple qu'avec deux condensateurs ou deux bobines ?
Un circuit RLC conduit toujorus à une équa diff du second degré:
donc soit tu as un truc du genre ...d²../dt²... + ...d.../dt + ...f(t)=g(t)
soit tu as un truc du genre ... ..dt + ... + ...d.../dt + ...f(t)=g(t)
..dt + ... + ...d.../dt + ...f(t)=g(t)
Ah d'accord. On n'a jamais rencontré jusque là le deuxième type. Et dans mon cas, je ne peux pas obtenir quelque chose de la première forme ?
Oui, j'ai compris. Mais, vous, vous obtenez une équa diff du second degrés avec une intégrale. Est-il possible, à partir de mon schéma d'obtenir une équa diff du second degres sans intégrale (=primitive)?
U = 1/C * i2+ L/(R1*C)*i2 + R2*i2 + L(R1+R2)/R1*di2/dt
i2+ L/(R1*C)*i2 + R2*i2 + L(R1+R2)/R1*di2/dt
= 1/C*q2+ L/(R1*C)*dq2/dt + R2*i2 + L(R1+R2)/R1*d²q2/dt²
avec q2(t) la charge du condensateur
La charge correspond-elle à la tension aux bornes du condensateur ? Sinon, je ne vois pas du comment obtenir cette équa diff, car je ne connais presque aucune formule contenant cette charge
Méthode de Laplace :
calcul de Z total sur le générateur.
Z = pL + [R1.(1 + pCR2)]/[pCR1 + (1 + pCR2)]
Z = [pL(pCR1 + (1 + pCR2)) + R1.(1 + pCR2)]/[pCR1 + (1 + pCR2)]
Z = [p²CR1L + pL + p²CR2L + R1+ pCR1R2)]/(1 + pC(R1+R2))
Z = [p²LC(R1+R2) + p(L + R1R2C) + R1]/(1 + pC(R1+R2))
U = Z * i
U = [p²LC(R1+R2) + p(L + R1R2C) + R1]/(1 + pC(R1+R2)) * i
(1 + pC(R1+R2))*U = [p²LC(R1+R2) + p(L + R1R2C) + R1] * i
U + (R1+R2).C.dU/dt = LC(R1+R2).d²i/dt² + (L + R1R2C).di/dt + R1.i
-----
Autrement :
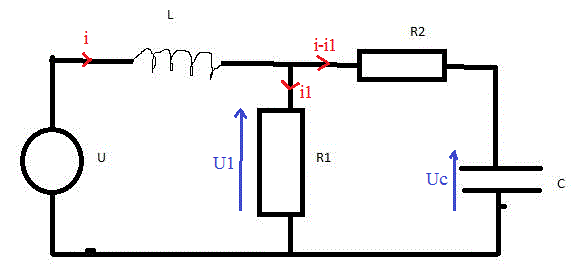
U = L.di/dt + U1
U1 = R1.i1
U1 = R2(i-i1) + Uc
i-i1 = C.dUc/dt
Eliminer U1 :
U = L.di/dt + R1.i1
R1.i1 = R2(i-i1) + Uc
i-i1 = C.dUc/dt
---
Eliminer i1 :
R1.i1 = R2(i-i1) + Uc
i1(R1+R2) = R2.i + Uc
i1 = (R2.i + Uc)/(R1+R2)
U = L.di/dt + R1.(R2.i + Uc)/(R1+R2)
i - (R2.i + Uc)/(R1+R2) = C.dUc/dt
---
Eliminer Uc :
U = L.di/dt + R1.(R2.i + Uc)/(R1+R2)
Uc.R1/(R1+R2) = U - L.di/dt - R1.R2.i/(R1+R2)
Uc = ((R1+R2)/R1).[U - L.di/dt] - R2.i
i - (R2.i + Uc)/(R1+R2) = C.dUc/dt
i - (R2.i + (R1+R2)/R1.(U - L.di/dt) - R2.i)/(R1+R2) = C.((R1+R2)/R1).(dU/dt - L.d²i/dt²) - R2.C.di/dt
i - (1/R1).(U - L.di/dt) = C.((R1+R2)/R1).(dU/dt - L.d²i/dt²) - R2.C.di/dt
R1.i - (U - L.di/dt) = C.(R1+R2).(dU/dt - L.d²i/dt²) - R1.R2.C.di/dt
R1.i - U + L.di/dt = C.(R1+R2).dU/dt - LC(R1+R2).d²i/dt² - R1.R2.C.di/dt
U + C.(R1+R2).dU/dt = R1.i + L.di/dt + LC(R1+R2).d²i/dt² + R1.R2.C.di/dt
U + (R1+R2).C.dU/dt = LC(R1+R2).d²i/dt² + (L + R1R2C).di/dt + R1.i
-----
Sauf distraction. 
Wahou, merci beaucoup ! Votre méthode est assez pertinente ! Avez-vous un ordre précis à me suggérer pour éliminer les composante ? Où la méthode marche dans tous les cas?
On élimine dans l'ordre qu'on veut ...
Mais il vaut mieux choisir un ordre qui s'arrange bien.
Voilà un autre ordre d'élimination par exemple :
U = L.di/dt + U1
U1 = R1.i1
U1 = R2(i-i1) + Uc
i-i1 = C.dUc/dt
Eliminer i1 :
U = L.di/dt + U1
U1 = R2(i- U1/R1) + Uc
i- U1/R1 = C.dUc/dt
---
Eliminer Uc :
U = L.di/dt + U1
i- U1/R1 = C.d[U1 - R2(i- U1/R1)]/dt
U = L.di/dt + U1
i- U1/R1 = C.dU1/dt - R2C.di/dt + (R2.C/R1).dU1/dt
-----
Eliminer U1
i- (U-L.di/dt)/R1 = C.(dU/dr-L.d²i/dt²) - R2C.di/dt + (R2.C/R1).(dU/dr-L.d²i/dt²)
R1.i- (U-L.di/dt) = R1.C.(dU/dr-L.d²i/dt²) - R1R2C.di/dt + (R2.C).(dU/dr-L.d²i/dt²)
R1.i- (U-L.di/dt) = (R1+R2).C.(dU/dr - L.d²i/dt²) - R1R2C.di/dt
R1.i- U + L.di/dt = (R1+R2).C.dU/dr - (R1+R2)LC.d²i/dt² - R1R2C.di/dt
U + (R1+R2).C.dU/dr = R1.i + L.di/dt + (R1+R2)LC.d²i/dt² + R1R2C.di/dt
U + (R1+R2).C.dU/dt = LC(R1+R2).d²i/dt² + (L + R1R2C).di/dt + R1.i


