Inscription / Connexion Nouveau Sujet
Eq diff en régime sinusïdal forcé
Bonjour à tous,
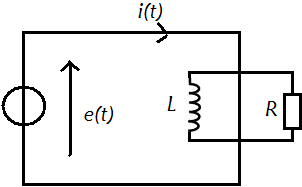
j'ai beau chercher, je ne trouve pas une eq. diff correcte pour trouver Im dans ce système. [voir image ci-dessous]
Je sais que e(t)=Eocos(Wt) et i(t)=Imcos(Wt+Y) et on est en régime sinusoidal forcé
Merci de votre aide!
Bonjour,
Il y a un problème avec votre schéma, la source de tension est court-circuité.
Sinon, la méthode est toujours la même, loi des noeuds, loi des mailles.... si votre circuit est celui auquel je pense (c'est à dire, le même mais sans le court-circuit en parallèle avec L et R), alors la tension aux bornes de la self est égale à celle aux bornes de la résistance, égales toutes deux e(t) (1ère équation) et la somme des courants dans chaque branche est égale à i(t) (2ème équation). On arrange un peu et ça doit marcher sans problème.
oui je me suis trompé le circuit ressemblait plus a ça...!
Il faut trouver deux equations et les rassembler c'est bien ça ?
Re,
OK, c'est bien comme ça que je voyais le circuit 
Alors, pour les équations, oui, si on vous demande une équation différentielle vérifiée par le courant, il faut faire comme je vous ait dit.
En fait, c'est même un peu plus simple.
La loi des noeuds donne (avec des notations qui me semblent explicites, mais si vous avez un doute, demandez).
Ensuite, vous connaissez et
, et vous pouvez exprimer les deux tensions
et
en fonction chacune de
et
. Puis vous remplacez, directement ou après une petite opération mathématique au vol, dans l'équation de la loi des noeuds et vous obtenez votre équation différentielle.
Vous voyez ? Je ne voudrais pas faire l'exercice à votre place.... j'en ai peut être déjà trop écrit....
Z = jwLR/(R + jwL)
|Z| = wLR/V(R²+w²L²)
arg(Z) = Pi/2 - arctg(wL/R)
i = Eo * [V(w²L²+R²)/(wLR)] .cos(wt - (Pi/2 - arctg(wL/R)))
i = Eo * [V(w²L²+R²)/(wLR)] .cos(wt - arctg(R/(wL))
-----
Autrement, par le chemin des écoliers ...
Si on veut vraiment passer par une équation différentielle (ce qui n'est pas vraiment utile dans le cas présent):
e = L.di(L)/dt
i(R) = e/R
i = i(L) + i(R)
di/dt = di(L)/dt + di(R)/dt
di/dt = e/L + (1/R).de/dt
Eq diff qu'on pouvait aussi trouver à partir de :
Z = jwLR/(R + jwL)
e = Z.i
e = jwLR/(R + jwL) . i
et avec jw = d/dt ... -->
R.e + L.de/dt = RL.di/dt
di/dt = e/L + (1/R).de/dt
Et ensuite, avec e = Eo.cos(wt), il vient :
di/dt = (Eo/L).cos(wt) - (w/R).Eo.sin(wt)
i = (Eo/(wL)).sin(wt) + (Eo/R).cos(wt) + K
Comme i , une fois le transitoire éventuel terminé, ne peut pas avoir de composante continue ---> K = 0
i = (Eo/(wL)).sin(wt) + (Eo/R).cos(wt)
Qui peut aussi s'écrire : i = Eo * [V(w²L²+R²)/(wLR)] .cos(wt - arctg(R/(wL))
-----
Recopier sans comprendre est inutile.
Sauf distraction. 
Bonjour J-P,
Merci pour le manque de respect que vous venez de manifester.
A quoi ça sert d'essayer de faire réfléchir les étudiants ?
Ceci est mon dernier post sur ce forum.


