Inscription / Connexion Nouveau Sujet
Énigme de trigo -- Projet de technologie
Bonjour,
Je fais la conception d'un projet pour l'école et je tombe sur ce problème:
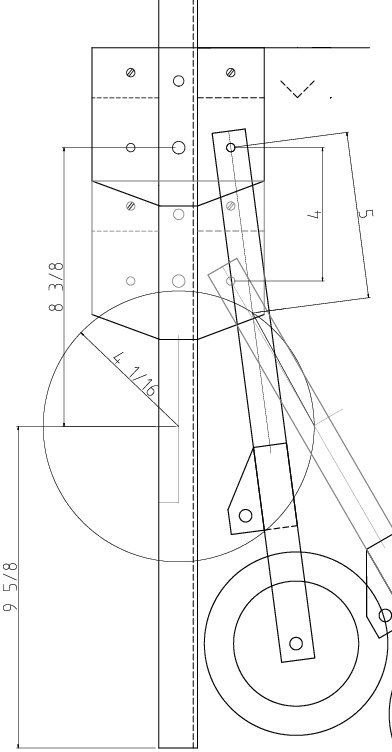
En image:
***
Je cherche la longueur de la barre de soutient (a=?). Malheureusement, je n'ai aucune idée sur la façon de résoudre ce problème.
Cordialement,
Charles
Ps: sur l'image, les deux croquis en haut sont inversés. Celui de droit devrait être à gauche et vice-versa.
édit Océane
Bonsoir,
Il ne faut pas mettre de lien externe (souvent très volatile) vers une image.
Pour apprendre à insérer une image, une figure, un schéma, un graphique, un tableau (pas un énoncé !) clique sur la maison 
![]() [lien]
[lien]

Tu n'exprimes pas très clairement ton problème.
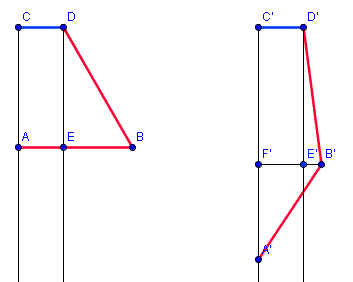
J'ai traduit sur ce schéma ce que j'en ai compris.
1ère position :
Puisque le triangle rectangle EDB est un demi triangle équilatéral et EB = DB/2
en conséquence AB = CD + (DB/2)
2ème position
E'B' = D'B' * sin(7,5°)
Et donc F'B' = C'D' + E'B'
C'F ' = D'E' = D'B' * cos(7,5°)
F 'A' se calcule par le théorème de Pythagore
F 'A' =  (A'B'2 - F 'B'2)
(A'B'2 - F 'B'2)
C'A' = C'F ' + F'A'
Toutes les coordonnées de tous les points peuvent donc être calculées ainsi que toutes les longueurs.

Merci beaucoup de ton aide, je t'en suis très reconnaissant.
Malheureusement, je bloque encore. Je connais la mesure de CD (donc AE aussi), de AF, des deux angles comme sur mon croquis. Après, je ne sais plus quoi faire même après avoir bien étudié ton explication.
Je pourrais essayer d'estimer les mesures avec un compas sur un dessin à l'échelle (Est-ce possible?), bien que je risque d'avoir une marge d'erreur assez importante comme mon prototype sera assez gros (les unités sont des pouces).
Ps: Je n'ai pas encore étudié les identités trigonométrique sinus et cosinus  On va les voir dans quelques mois.
On va les voir dans quelques mois.
Attention il n'y a pas de segment AF dans mes figures.
Donne (sans te tromper) toutes les dimensions que tu connais
Il faut au minimum : CD, DB et AB

A'F'=4
C'D'= CD = AE = F'E' =1.5
angle EDB = 30°
angle E'D'B'= 7,5°
Ton schéma donne toutes les autres infos (angles droits, segments parallèles...).
Je ne comprends toujours pas... désolé...
Est-ce que le point A est un point fixe (et donc A = A') et que tu souhaites que le point C se lève de 4 ?
Si c'est ce que tu veux, alors il faut imposer que C'A' - CA = 4
Mais ce n'est pas en écrivant A'F ' = 4 que tu obtiendras ce résultat parce que CA n'est pas égal à C'F '
Que veux-tu exactement ?

ah ok... CA doit égaler CF. Par apport au dessin original, A se déplace de 4 u vers vers le bas sur C'F', mais AB=A'B' et DB=D'B'. Il n'y a que A et B qui se déplacent.
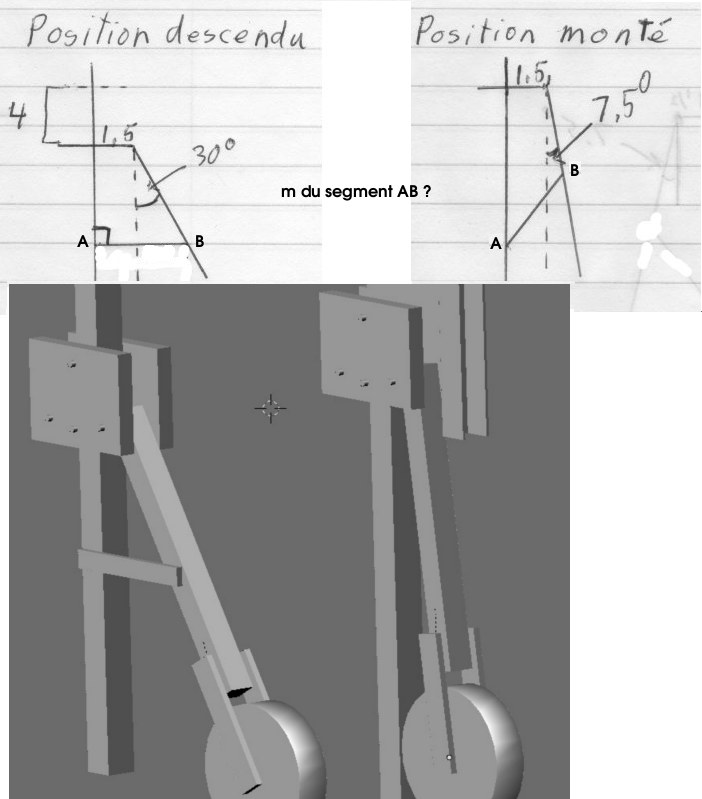
Finalement, j'ai trouvé un moyen d'estimer la mesure de AB sur dans mon logiciel de CAO. Les traits plus fin représentent la position baissé. Une barre de métal (AB) doit relier le centre du cercle et le centre de l'autre barre situé sur son rayon du cercle.
Je te remercie grandement de ton aide. Je n'ai pas trouvé la solution de façon arithmétique, mais j'ai pu l'estimer en géométrie.