Bonsoir.

Ce que tu dis est correct. Le théorème de l'énergie cinétique montre que, puisque F ne travaille pas, alors cette force n'accélère pas la particule.
On peut faire un PFD :
dv/dt = ku^v
Il y a un produit vectoriel, donc on raisonne avec les coordonnées.
On choisit un bon repère cartésien, c'est-à-dire un dont l'un des axes dirige u, pour simplifier les équations.
On devrait normalement trouver deux équations couplées, et une équation résolue.
Pour découpler les équations, plusieurs méthodes : on peut dériver ou intégrer les équations pour découper, ou alors poser la variable t=x+iy si les variables couplées sont x et y (ici les variables couplées seront les coordonnées de la vitesse selon deux directions précises).
À rapprocher de l'étude de la trajectoire dans un champ magnétique stationnaire uniforme.

Bonsoir,
Merci de votre réponse.
J'ai tenté de raisonner sur les coordonnées donc j'obtiens les coordonnées du vecteur f en fonction de celles des vecteurs u et v.
Après je ne comprends pas votre formule du PFD: pourquoi la masse n'y apparait elle pas?

Parce que je l'ai oubliée

Ha en effet! xD Je pensais que c'était en rapport avec le fait que vous ne considériez pas le poids de la particule!

Bon avec les coordonnées, j'ai:
(cf image)
Ensuite, avec le pfd:
g+ k/m u v =dv/dt
Comment projeter le produit vectoriel pour pouvoir projeter cette relation sur les 3 axes, et obtenir 3 équations?
Merci d'avance.

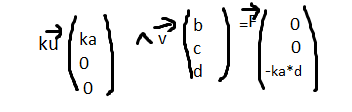
Je pense qu'il est sous-entendu que la seule force est F, donc pas de poids à mon avis, donc g disparaît.
On a : dv/dt = (k/m)u^v
On choisit le repère (x,y,z) tel que u soit porté par x.
Alors u=(u,0,0), et v=(Vx,Vy,Vz)
Et u^v=(0,-uVz,uVy)
et dv/dt = (dVx/dt,dVy/dt,dVz/dt)
On en déduit :
dVx/dt = 0
dVy/dt = -(ku/m)Vz
dVz/dt = (ku/m)Vy
La première équation se résout : Vx=constante
Les deux suivantes sont couplées : on peut par exemple introduire la variable h=Vy+iVz avec i le nombre complexe : i²=-1
Alors dh/dt = dVy/dt + idVz/dt
En notant w=ku/m :
dh/dt = -wVz + iwVy = (Vy+iVz)*w*i=hwi
Donc dh/dt = (iw)*h, ce qui se résout en h=Aexp(iwt), avec A a priori complexe, donc A=a+ib, à déterminer avec les conditions initiales.
On en déduit Vy et Vz en identifiant parties réelle et imaginaire de h.

Bonjour,
Merci beaucoup de votre réponse!
Je comprends un petit peu mieux, mais j'avoue que je suis dans le flou pour la résolution des deux équations couplées ... :/
Je comprends comment vous l'avez fait et je vois bien que ça fonctionne, mais après comment savoir qu'il faut faire ça?
(bon maintenant je le sais mais, c'est souvent mon problème ça :/)

Parce que c'est classique.
On aurait pu aussi dériver les équations :
d²Vy/dt²=-wdVz/dt=-w²Vy : hop une équation différentielle du second ordre, on en déduit Vy, idem pour Vz.
On peut aussi raisonner avec la coordonnée y :
wVy=dVz/dt donc Vy=(1/w)dVz/dt puis on intègre : y=(1/w)Vz+c (c : constante)
donc y=(1/w)(-1/w)dVy/dt + C
soit y=(-1/w²)d²y/dt² + c, équation du second ordre en y qu'on peut résoudre.

En gros ya du boulot!
Merci beaucoup

bonsoir,

je ne pense pas qu'il y ait besoin de bcp de calculs.

on remarque que: d/dt(.) = .d/dt (car est un vecteur constant)

or l'accélération est normale à (puisque F l'est, et F = ma)

donc .d/dt = 0

d/dt(.) = 0
. est donc constant

or . = |||| |||| cos(,)

et comme |||| est constante et |||| = 1

cos(,) est donc constant

tout ça pour dire que la tangente à la trajectoire en tout point fait un angle constant avec une direction fixe (celle de ),

ce qui est la définition géométrique d'une ....

sauf erreur